Уравнение плоской гармонической волны

Уравнением волны называется выражение, которое определяет смещение колеблющейся частицы как функцию координат и времени.

Найдем вид уравнения для плоской гармонической волны.

Пусть в начале координат находится источник плоских волн, которые распространяются вдоль оси x. Смещение точек среды в плоскости x = 0 совершается по гармоническому закону:

.

Найдем вид функции, описывающий колебания точек в некоторой плоскости x. Для того, чтобы волна прошла путь от источника до точки наблюдения, требуется время , где v - фазовая скорость распространения волны (рис. 3.5).

Рис.3.5

Поэтому уравнение колебаний частиц, лежащих в плоскости x, будет иметь вид

Приведем это уравнение к симметричному виду:

.

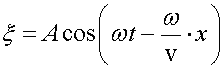Найдем, чему равно отношение 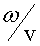, используя формулы (3.3), (3.20) и (3.22):

где k - волновое число.

Тогда получим уравнение плоской волны:

где A - амплитуда волны,
- фаза волны, т. е. фаза колебаний в точке с координатой x.

Формула (3.18) показывает, что смещение ξ зависит от времени t и координаты x - координаты положения равновесия колеблющейся частицы среды.

Рис.3.6

На рис. 3.6 представлен график зависимости смещения от координаты при t = const (формула (3.24)). На этом рисунке показаны амплитуда волны A и длина волны λ.