Сложение гармонических колебаний одинакового направления и одинаковой частоты

Пусть надо сложить два колебания, которые определяются уравнениями

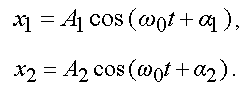
Представим каждое колебание в виде вектора и найдем по правилам сложения векторов результирующий вектор (рис. 3.4).

Рис.3.4

Результирующее колебание равно сумме складываемых колебаний, т. е.

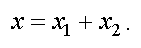
Так как угловая скорость ω ₀ у складываемых векторов одинакова, то результирующий вектор тоже вращается со скоростью ω ₀. Тогда уравнение результирующего колебания имеет вид

Результирующую амплитуду можно найти по теореме косинусов

По формулам приведения в тригонометрии

Тогда квадрат результирующей амплитуды равен

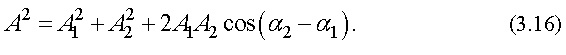
Результирующая амплитуда равна

Начальная фаза результирующего колебания находится из выражения для тангенса угла α:

Значение угла α можно найти из следующего равенства

Проанализируем выражение для амплитуды (3.17). Это выражение показывает, что значение амплитуды результирующего колебания зависит от разности фаз складываемых колебаний.

Если разность фаз (α ₂ - α ₁) = 2 nπ, где n = 0, 1, 2,..., то A = A ₁ + A ₂ - это максимальное значение для результирующей амплитуды. Если разность фаз (α ₂ - α ₁) = (2 n+ 1) π, где n = 0, 1, 2,..., то A = A ₁ - A ₂ - это минимальное значение амплитуды. Следовательно, колебания в зависимости от разности фаз могут усиливать или ослаблять друг друга. Этот важный вывод используется при описании интерференции волн.

Волны