Дифференциальное уравнение гармонических колебаний

Составим дифференциальное уравнение гармонических колебаний на примере пружинного маятника (рис. 3.2) (m - масса маятника, k - коэффициент упругости пружины). Сила, действующая на тело, закрепленное на пружине, находится по закону Гука (см. (1.20)). Эта сила направлена против смещения

где k - коэффициент упругости, x - смещение тела от положения равновесия.

Рис.3.2

Уравнением движения тела будет II закон Ньютона (1.22)

,

где - результирующая сила равна силе упругости;
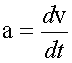- ускорение тела (см. формулу (1.8));
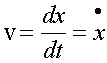- скорость тела (см. формулу (1.5)).

Производная по времени обозначается точкой сверху.

Тогда ускорение тела равно второй производной от координаты по времени

.

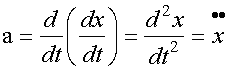Подставим выражения для силы упругости и для ускорения в формулу II-го закона Ньютона и получим

.

Преобразуем это уравнение

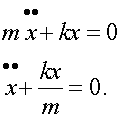
Введем обозначение

где 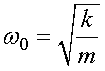- частота собственных незатухающих колебаний.

Собственными колебаниями называются колебания, которые совершает система, выведенная из положения равновесия и предоставленная самой себе. Собственные колебания бывают незатухающими и затухающими. В нашем примере мы рассматриваем незатухающие колебания. С учетом обозначений получим дифференциальное уравнение гармонических колебаний:

Дифференциальное уравнение гармонических колебаний имеет такой же вид для любых других величин, изменяющихся по гармоническому закону.

С точки зрения математики уравнение (3.8) представляет собой однородное дифференциальное уравнение второго порядка. Решение его находится, например, путем подбора функции, которая обращает дифференциальное уравнение в тождество. Решение уравнения (3.8) представляет собой уравнение гармонических колебаний

или