 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Частные случаи движения точки
|
|
Рассмотрим сведенные к таблице 1 случаи характера движения точки в зависимости от значений касательного и нормального ускорений.
Таблица 1
| Характер движению точки | Значение ускорения | Траектория, векторы скорости и ускорения, кинематические зависимости | ||
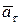
| 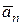
| 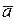
| ||
| Равномерное прямолинейное движение | 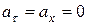
| 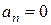
| 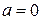
|   
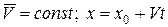
|
| Равноперемен-ное прямолинейное | 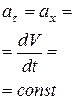
| 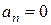
| 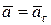
| 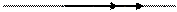
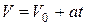
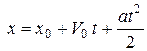
|
| Равномерное криволинейное | 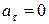
|
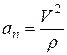
| 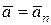
| 
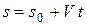
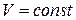
|
| Равноперемен-ное криволинейное | 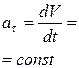
| 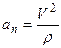
| 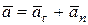
| 
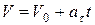
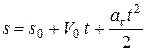
|
Как видим, только в случае равномерного прямолинейного движения точки ее ускорения равняются нулю. В других частных случаях движения точка имеет отличающееся от нуля ускорение: при переменном прямолинейном движении ускорение точки будет только касательным, при равномерном криволинейном – только нормальным, а при переменном криволинейном движении ускорения точки будет состоять из касательного и нормального ускорений.
Следует отметить, что касательное ускорение равняется нулю при движении точки с постоянной алгебраической скоростью, или в моменты времени, когда алгебраическая скорость приобретает экстремальные значения (максимум или минимум).
Нормальное ускорение будет равняться нулю при прямолинейном движении или в местах перегиба траектории, то есть когда 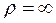 , а также в те моменты времени, когда скорость точки равняется нулю.
, а также в те моменты времени, когда скорость точки равняется нулю.
Дата публикования: 2015-09-17; Прочитано: 758 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
