Сложение натуральных чисел

Сложением натуральных чисел называется бинарная операция, удовлетворяющая следующим двум аксиомам:

С1: а + 1 = а^/

С2: а + b^/ = (a + b)^/

Пример. Найдём на основании определения сумму 2 + 2:

2 + 2 = 2 + 1^/ = (2 + 1)^/ = (2^/)^/ = 3^/ = 4.

Теорема 1 (о существовании и единственности сложения). Каждой паре натуральных чисел а и b соответствует однозначно определённая сумма а + b, удовлетворяющая определению сложения (аксиомам С1 и С2).

Доказательство. Единственность. Предположим, что наряду с операцией +, удовлетворяющей условиям С1 и С2, существует также другая операция Å, удовлетворяющая условиям С1^/ и С2^/:

С1^/: а Å 1 = а^/

С2^/: а Å b^/ = (a Å b)^/

Тогда для любых натуральных чисел справедливо равенство: а + b = a Å b.

Доказательство проведём методом математической индукции по переменной b. При b = 1 на основании С1 и С1^/ получаем:

a + 1 = a^/ = a Å 1

Таким образом, при b = 1 данное свойство справедливо.

Индукционное предположение: a + k = a Å k

Докажем данное утверждение при b = k^/:

На основании С2 a + k^/ = (a +k)^/

Из индукционного предположения на основании аксиомы А₂ из определения натуральных чисел a + k = a Å k => (a + k)^/ = (a Å k)^/, откуда по условиям С2 и С2^/ имеем:

a + k^/ = (a +k)^/ = (a Å k)^/ = a Å k^/,

что и требовалось.

Существование. Введённое индуктивное определение позволяет найти сумму для любого второго слагаемого (элемента b). Выясним, можно ли найти сумму для любого первого слагаемого (элемента а). Для этого сами введём операцию, удовлетворяющую условиям (*) и (**)

(*) 1 + b = b^/

(**) а^/ + b = (a +b)^/.

Докажем, что введённая нами операция является сложением, то есть удовлетворяет условиям С1 и С2. Доказательство будем проводить индукцией по а.

Начнем с доказательства С1. База индукции: Для а = 1

1 + 1 = 1^/ (на основании условия (*)).

Индукционное предположение: k + 1 = k^/

Шаг индукции: Для а = k^/ требуется доказать, что k^/ + 1 = (k^/)^/.

На основании условия (**) k^/ + 1 = (k+1)^/ = (k^/)^/ (по индукционному предположению). Таким образом, условие С1 выполняется для всех натуральных а.

С2: Для а = 1 по условию (*) 1 + b^/ = (b^/) ^/ = (1 + b)^/.

Индукционное предположение (и.п.): k + b^/ = (k +b)^/.

Для а = k^/ требуется доказать, что k^/ + b^/ = (k^/ + b)^/.

Здесь над каждым равенством указано обоснование – свойство, на основании которого данное равенство выполняется. Таким образом, условие С2 также выполняется для всех натуральных а. Теорема полностью доказана.

Теорема 2. Для любых натуральных чисел а, b, c выполняется ассоциативный закон сложения (а.з.с.): (a + b) + c = a + (b +c)

Доказательство (индукцией по с): При с = 1 имеем:

Индукционное предположение: (a+b)+k = a+(b+k).

Согласно принципу индукции теперь требуется доказать, что

(a+b)+k^/ = a+(b+k^/). Докажем это.

Таким образом, для k^/ утверждение справедливо, следовательно, согласно теореме индукции, ассоциативный закон справедлив для любых натуральных чисел.

Теорема 3. Для любых натуральных чисел выполняется коммутативный закон сложения (к.з.с.) a + b = b + a

Доказательству теоремы предпошлём лемму.

Лемма 1. a + 1 = 1 + a (Л1)

Докажем её индукцией по а. База индукции: 1 + 1 = 1 + 1 (справедливо)

Индукционное предположение: k + 1 = 1 + k.

Шаг индукции: Докажем, что k^/ + 1 = 1 + k^/.

Лемма доказана.

Теперь докажем саму теорему индукцией по b. Для b = 1 утверждение теоремы истинно по лемме 1.

Индукционное предположение: a + k = k + a.

Шаг индукции:

Отсюда, утверждение справедливо и для k^/, что доказывает нашу теорему.

Теорема 4. Сумма двух чисел не равна ни одному из слагаемых:

a + b ¹ b.

Доказательство индукцией по b: Для b = 1 утверждение теоремы истинно по аксиоме 1 из определения натуральных чисел (a^/ ¹ 1).

Индукционное предположение: a + k ¹ k.

Из индукционного предположения и теоремы 1 пункта 1.2 следует, что (а + k)^/ ¹ k^/. Применяя С2, получаем:

а + k^/ = (а + k)^/ ¹ k^/.

Теорема 5. а = b => a + c = b + c.

Доказательство (индукцией по с):

а = b => (по А₂) a^/ = b^/ => (по С1) а + 1 = b +1.

Индукционное предположение: a = b => a + k = b+k.

Докажем, что a = b влечёт за собой a + k^/ = b + k^/.

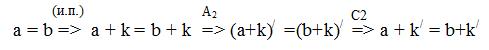
Таким образом, для k^/ утверждение справедливо, следовательно, согласно теореме индукции, теорема справедлива для любых натуральных чисел.

Следствие 1. a + с ¹ b + с = > a ¹ b (доказательство проводится методом от противного и предоставляется читателю).

Теорема 6. a + c = b + c => а = b.

Доказательство (индукцией по с):

а + 1 = b + 1 => a^/ = b^/ => а = b (по С1 и А₃).

Индукционное предположение: a + k = b + k => a = b.

Докажем, что a + k^/ = b + k^/ влечёт за собой a = b.

Отсюда, утверждение справедливо и для k^/, что доказывает нашу теорему.

Следствие 2. a ¹ b = > a + с ¹ b + с (доказательство методом от противного).

Решением уравнения а + х = b (а, b – натуральные числа, х – переменная) называется такое натуральное число с, при подстановке которого вместо х в уравнение, получается верное числовое равенство а + с = b

Теорема 7. Если уравнение а + х = b имеет решение, то это решение единственно.

Доказательство: Предположим, что существуют два решения с₁ и с₂. Тогда а + с₁ = b и а + с₂ = b, откуда а + с₁ = а + с₂, а по теореме 6 и коммутативному закону это означает, что с₁ = с₂ (то есть решение единственно).

Задания для самостоятельного решения

№ 1.2. Сложить на основании определения сложения натуральных чисел 5 + 3. Выполнить то же действие в представленных ниже моделях натуральных чисел

а) {3, 4, 5 …}; n^/ = n +1

б) {n ³ –2, n Î Z }; n^/ = n +1

в) нечётные натуральные числа, n^/ = n +2

г) Целые числа,

№ 1.3. Докажите равенства для любого натурального n:

а) 1 + 2 + …+ n = ;

б) 1² + 2² + … + n² = ;

в) 1³ + 2³ + … + n³ = ;

г) 1 + 3 + 5 + … + (2n + 1) = (n + 1)²;

д) 1² + 3² + … + (2n – 1)² = ;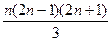

e) 1×2 + 2×3 + … + (n – 1)×n = ;

ж) ;

з) .