Умножение натуральных чисел

Умножением натуральных чисел называется бинарная операция, удовлетворяющая следующим двум аксиомам:

У1: а × 1 = а

У2: а × b^/ = a × b + а

Теорема 1. Для любых двух чисел а и b существует однозначно определённое произведение a×b, удовлетворяющее определению умножения.

1) Единственность. Предположим, что наряду с операцией × удовлетворяющей условиям У1 и У2 существует также другая операция *, удовлетворяющая условиям С1^/ и С2^/:

У1^/: а * 1 = а

У2^/: а * b^/ = a*b + а

Наша задача – доказать, что для любых натуральных чисел а × b = a * b. Доказательство проведём методом математической индукции по переменной b.

При b = 1: a × 1 = a = a * 1 (первое равенство на основании У1, второе – на основании У1^/). Таким образом, для единицы данное свойство справедливо.

Индукционное предположение: a × k = a * k

Докажем данное утверждение при b = k^/:

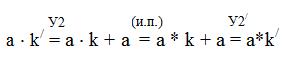
что и требовалось.

2) Существование. Введём операцию, удовлетворяющую условиям (*) и (**)

(*) 1 × b = b^/

(**) а^/ × b = ab +b.

Докажем, что введённая нами операция является умножением, то есть удовлетворяет условиям У1 и У2. Доказательство будем проводить индукцией по а.

У1: Для а = 1

1 × 1 = 1 (на основании условия (*)).

Индукционное предположение k × 1 = k.

Для а = k^/ требуется доказать, что k^/ × 1 = k^/.

На основании условия (**) k^/ × 1 = k×1 + 1 = k + 1 =k^/ (по индукционному предположению и С1). Таким образом, условие У1 выполняется для всех натуральных а.

У2: Для а = 1 по условию (*) 1× b^/ = b^/ = b + 1 = 1×b + 1.

Индукционное предположение k × b^/ = k ×b + k.

Для а = k^/ требуется доказать, что k^/ × b^/ = k^/ ×b + k^/.

На основании условия (**) k^/ × b^/ = k×b^/ + b^/ = (kb + k) + b ^/ (по индукционному предположению). В свою очередь,

(kb + k) + b ^/ = kb + (k + b ^/) = kb + (k + b) ^/ = kb + (b + k) ^/ = kb + (b + k^/) =

= (kb + b) + k^/ = k^/ ×b + k^/.

Таким образом, условие У2 также выполняется для всех натуральных а. Теорема полностью доказана.

Найдём на основании определения произведение 2×2:

2 × 2 = 2 × 1^/ = 2×1 + 2 = 2 + 2 = 4.

Теорема 2. Для любых натуральных чисел а, b, c выполняется дистрибутивный закон (ДЗ1): (a + b)×c = a×с + b×c.

Доказательство (индукцией по с):

(a + b)×1 = (a + b) = a×1 + b×1 (на основании У1).

Индукционное предположение: (a+b)×k = a×k + b×k.

Докажем, что (a+b)×k^/ = a× k^/ + b×k^/. Действительно

(a+b)×k^/ = (a+b)×k + a + b = a×k + b×k + a + b = (a×k + a) + (bk + b) = a×k^/ + b×k^/.

Таким образом, для k^/ утверждение справедливо, следовательно, согласно теореме индукции, дистрибутивный закон справедлив для любых натуральных чисел.

Теорема 3. Для любых натуральных чисел выполняется коммутативный закон умножения a × b = b × a.

Доказательству теоремы предпошлём лемму.

Лемма 2. a × 1 = 1 × a (Л2)

Доказательство индукцией по а: 1 × 1 = 1 × 1 (справедливо).

Индукционное предположение: k × 1 = 1 × k.

Докажем, что k^/ × 1 = 1× k^/.

Лемма доказана.

Теперь докажем саму теорему индукцией по b. Для b = 1 утверждение теоремы истинно по лемме 2.

Индукционное предположение: a × k = k × a.

Шаг индукции:

Таким образом, для k^/ утверждение справедливо, следовательно, согласно теореме индукции, коммутативный закон доказан для любых натуральных чисел.

В теореме 2 мы доказали одну из форм дистрибутивного закона. Теперь мы имеем возможность доказать и вторую форму дистрибутивного закона.

Теорема 4. Для любых натуральных а, b, c: a×(b + c) = a×b + a×c (ДЗ2).

Доказательство: a×(b + c) = (b + c)×а = b×а + c×а = a×b + a×c.

Теорема 5. Для любых натуральных чисел а, b, c выполняется ассоциативный закон умножения: (a × b) × c = a × (b × с)

Доказательство (индукцией по с):

(a × b) × 1 = a × b = a × (b ×1).

Индукционное предположение: (a×b)×k = a×(b×k).

Докажем, что (a×b)×k^/ = a×(b×k^/)

(a×b)×k^/ =((a×b)×k) + a×b = a×(b×k) + a×b = a×(b×k + b) = a×(b×k^/).

(пояснения расставьте самостоятельно). Таким образом, для k^/ утверждение справедливо, следовательно, теорема доказана.

Теорема 6. а = b => a × c = b × c.

Доказательство (индукцией по с): а = b => а ×1 = b ×1 (по У1).

Индукционное предположение: a = b => a×k = b×k.

Докажем, что a = b влечёт за собой и a × k^/ = b × k^/.

a = b => a × k = b × k. Прибавим к правой и левой части а:

a × k + а = b × k + а.

Так как по условию a = b, сделаем замену в правой части равенства:

a × k + а = b × k + b откуда по У2: a×k^/ = b×k^/

Таким образом, для k^/ утверждение справедливо, следовательно, согласно теореме индукции, теорема справедлива для любых натуральных чисел.

Следствие 1. a × с ¹ b × с => a ¹ b (доказательство методом от противного).

Закон сокращения для умножения будет доказан в следующем параграфе.

Задания для самостоятельного решения

№ 1.4. Умножить на основании определения числа 5 и 3. Выполнить то же действие в представленных ниже моделях натуральных чисел

а) {3, 4, 5 …}; n^/ = n +1

б) {n ³ - 2, n Î N }; n^/ = n +1

в) нечётные положительные числа, n^/ = n +2

г) Целые числа,

№ 1.5. Расставьте над знаками равенств в теореме 5 все обоснования.

№ 1.6. Введём в рассмотрение операцию суммирования n натуральных чисел () по следующему правилу:

1) при n = 1: , 2) при n = k + 1: .

Если считать, что все а_i равны между собой и равны а, то построенную сумму будем называть n-кратным числа а и обозначать символом «na»:

1) 2)

Докажите, что натуральное n-кратное числа а совпадает с произведением а×n.

№ 1.7. Докажите, что для любого натурального n

а) n³ – n делится на 3; д) n⁷ – n делится на 7;

б) n⁵ – n делится на 5; е) 3²ⁿ + 2^{6n – 5} делится на 11;

в) 3²ⁿ⁺¹ + 2ⁿ⁺² делится на 7; ж) 3²ⁿ - 2ⁿ делится на 7.

г) 2²ⁿ⁺¹× 3ⁿ⁺³ + 1 делится на 11;