Особенности проблемы оптимизации управления иерархической двухуровневой системой

В проблеме оптимизации управления иерархической двухуровневой системой можно выделить следующие основные, имеющие самостоятельное значение, и в то же время взаимосвязанные классы задач:

- иерархического управления (на основе межуровневых и внутриуровневых взаимодействий подсистем);

- распределенного управления (с учетом внутриуровневых взаимодействий равнозначных подсистем);

- локального управления (без учета межуровневых и внутриуровневых взаимодействий).

Анализ многочисленной библиографии позволяет сделать вывод о значительном потенциале и перспективности игровых подходов к разработке методов исследования ССС, что обусловлено их универсальным характером

Как указывалось выше, теоретико-игровой подход, в силу его универсального характера, уже на этапе постановки задачи оптимизации управления ССС позволяет учитывать все виды неопределенных факторов: неопределенность цели, неопределенность среды, неопределенность поведения активного партнера.

Для определенности будем предполагать, что все участники конфликта стремятся минимизировать значения своих показателей эффективности.

Учитывая наличие приоритета действий подсистем верхнего уровня, а также обратной зависимости результатов действий подсистем верхнего уровня от фактического исполнения подсистемами нижнего уровня своих функций, задачу оптимизации управления иерархической двухуровневой системой целесообразно сформулировать в виде иерархической игры в условиях неопределенности с правом первого хода:

. (1.8)

Предполагается, что в игре (1.8) принимает участие игрок: координирующий центр и множество игроков (управляющих подсистем) , , нижнего уровня. О неопределенном факторе лишь известно, что он принимает значения из множества , – векторный показатель эффективности Центра; – бинарное отношение нестрогого предпочтения Центра на множестве достижимых векторных оценок .

Игра описывает условия конфликтного взаимодействия игроков (подсистем) нижнего уровня в условиях неопределенности при фиксированном .

Механизм формирования оптимального решения иерархической игры (1.8) является многоэтапным и может быть записан в следующем виде.

Этап 1. Первый ход делает Центр – он сообщает игрокам нижнего уровня свою стратегию 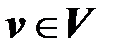. Далее при фиксированном игроки нижнего уровня разыгрывают игру в условиях неопределенности вида (1.9), формируя множество оптимальных решений. Конкретный вид множества зависит от условий конфликтного взаимодействия на нижнем уровне иерархии, а также от вида множества . Условия конфликтного взаимодействия на нижнем уровне могут быть заданы Центром, либо выбираются игроками нижнего уровня независимо от Центра (это может определяться техническими условиями, социально-экономическими, юридическими и другими факторами).

Этап 2. Центр оценивает эффективность применения стратегии в условиях неопределенности , после чего на множестве осуществляется построение множества оптимальных решений координирующего центра .

Задача оптимизации распределенного управления на нижнем уровне иерархии с учетом внутриуровневых взаимодействий при фиксированной стратегии Центра в достаточно общем виде может быть сформулирована, как коалиционная игра в условиях неопределенности [Вилкас, Воронов]:

. (1.9)

В (1.9) – некоторое семейство коалиций. Для членов коалиции характерны общность интересов и согласованный характер действий, то есть:

вектор объединяет компоненты векторов управления (стратегий) подсистем , образующих коалицию ;

- множество допустимых стратегий коалиции ;

- векторный показатель эффективности коалиции , где 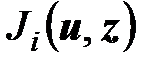- показатель эффективности управляющей подсистемы , (без потери общности и для простоты обозначений будем предполагать, что – скалярная величина);

- коалиционное транзитивное отношение нестрогого предпочтения, характеризующее интересы всей коалиции на множестве достижимых векторных оценок ; порождает отношение строгого предпочтения .

Считается, что игра (1.9) разыграна, если игроки разбились на коалиции, образовалась коалиционная структура , и все образующие ее коалиции выбрали свои стратегии.

Коалиционная структура представляет собой разбиение множества участников конфликта на коалиции:

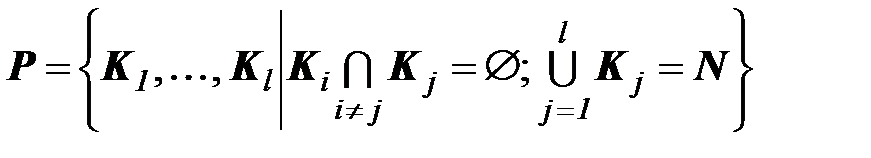. (1.10)

Конкретная конфигурация коалиционной структуры (1.10) позволяет учитывать следующие виды внутриуровневых взаимодействий подсистем: согласованное (кооперативное), несогласованное (бескоалиционное), коалиционное.

В зависимости от вида коалиционной структуры (1.10), определяющей структурно-целевую взаимосвязь подсистем ССС, а также от условий их информационного взаимодействия, решение задачи (1.9) возможно в рамках кооперативного, бескоалиционного, коалиционного подходов.

В основе каждого из перечисленных подходов лежит теоретико-игровая концепция равновесия, использующая три фундаментальных понятия теории игр: стабильность, эффективность и стабильно-эффективный компромисс [Воронов, Харш, Ж-Чикрий], и имеющая множество интерпретаций в виде конкретных принципов оптимальности в зависимости от уровня структурно-целевой и информационной сложности задачи (1.9).

Стабильность – это обеспечение устойчивости процессов функционирования и проектирования ССС в условиях конфликтности (несогласованности) и неопределенности.

Эффективность – это достижение максимального целевого качества подсистем, коалиций и ССС в целом.

Стабильно-эффективный компромисс – это сочетание свойств стабильности и эффективности в рамках множества решений – от обеспечения различной степени сближения до полного их совпадения в условиях информационно-тактических расширений.

Сравнение бескоалиционной, коалиционной и кооперативной концепций равновесия является основным принципом теоретико-игрового анализа ССС, а также источником строгих и вместе с тем содержательных рассуждений о побудительных мотивах поведения участников конфликта, вытекающих из структуры игровых моделей [].

Задача локального управления представляет собой частный случай постановки (1.9) и решается для отдельной коалиции в рамках заданной коалиционной структуры при фиксированных стратегиях контркоалиции (в настоящей работе эта задача интерпретируется, как задача многокритериальной оптимизации в условиях неопределенности).

Задачи оптимизации управления более сложными иерархическими многоуровневыми системами могут быть сформулированы на основе комбинирования вышеперечисленных постановок задач и развития теоретико-игровых принципов оптимальности в соответствии с понятиями стабильности и эффективности [Ж-Чикрий, Горелик, Ватель-Герм,].

Задача локального управления как задача многокритериальной оптимизации

Задача локального управления может решаться для отдельной подсистемы, а также для отдельной коалиции в рамках заданной коалиционной структуры при фиксированных стратегиях соответствующих контркоалиций. При этом предполагается, что внутри коалиции имеет место согласованный (кооперативный) характер взаимодействия подсистем, который проявляется в том, что все игроки (подсистемы) действуют совместно с целью увеличения своих выигрышей.

Для удобства обозначений будем предполагать, что подсистемы образуют единую коалицию . То есть в этом случае игру (1.9) можно рассматривать, как кооперативную.

В классической теории кооперативных игр изучаются в основном игры в форме характеристической функции. При этом основная проблема состоит в выборе дележа, распределяемого между игроками после завершения игры []. Отсутствие же прямых коммуникаций между управляющими подсистемами на уровне управления можно трактовать, как отсутствие дележа.

В указанном случае одной из основных интерпретаций постановки задачи (1.9) является ее формулировка в виде задачи многокритериальной оптимизации в условиях неопределенности:

. (1.11)

В (1.11) требуется минимизировать компоненты векторного показателя , заданного на прямом произведении множеств , где .

1.3.1 Детерминированная задача многокритериальной
оптимизации

Рассмотрим предварительно задачу (1.11) в детерминированном варианте, когда :

. (1.12)

Как известно, на множестве достижимых векторных оценок задачи (1.12) естественным образом можно ввести систему бинарных отношений нестрогого, строгого предпочтения и безразличия соответственно вида:

; (1.13)

; (1.14)

. (1.15)

Отношения (1.13)-(1.15) взаимосвязаны следующим образом: ; . Поэтому в постановке задачи (1.12) присутствует отношение .

Определение 1.1. Векторная оценка 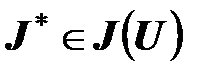называется минимальной (недоминируемой) по на множестве достижимых векторных оценок в задаче многокритериальной оптимизации (1.12), если не существует векторной оценки такой, что .

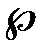Определение 1.2. Множество минимальных по объектов из называется внутренне устойчивым, если не может быть ни , ни .

Определение 1.3. Множество называется внешне устойчивым, если для всякого элемента , который не является минимальным, найдется более предпочтительный минимальный элемент , т.е. .

Определение 1.4. Внешне и внутренне устойчивое множество называется ядром отношения на множестве .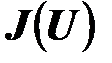

Определение 1.5. Векторная оценка , где отношение строгого предпочтения определено в виде (1.14), называется эффективной (оптимальной по Парето). Множество называется эффективным или множеством Парето и обозначается . Соответствующее допустимое решение называется эффективным (оптимальным по Парето) решением задачи (1.12). Множество эффективных решений обозначается .

На множестве достижимых векторных оценок задачи (1.12) можно определить отношение строго предпочтения в ином виде:

. (1.16)

Определение 1.6. Векторная оценка , где отношение строгого предпочтения определено в виде (1.16), называется слабо эффективной (оптимальной по Слейтеру). Множество называется слабо эффективным или множеством Слейтера и обозначается . Допустимое решение называется слабо эффективным (оптимальным по Слейтеру) решением задачи (1.12). Множество оптимальных по Слейтеру решений обозначается .

Легко показать, что .

В работах [Ю] развивается более общий подход к проблеме многокритериальной оптимизации, основанный на теории доминирования и использующий в качестве основных такие понятия, как структура доминирования, конус доминирования, оптимальность по конусу.

Определение 1.7. Каждому элементу поставим в соответствие множество , называемое множеством доминирующих факторов. Если таков, что и , то будем говорить, что элемент доминирует , (или предпочтительнее, чем ).

Совокупность 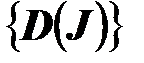, определенная на всем множестве , называется структурой доминирования.

Определение 1.8. Пусть - замкнутый выпуклый конус, с вершиной в точке . Если таков, что и , то будем говорить, что элемент доминирует относительно конуса доминирования .

Таким образом, с помощью замкнутого выпуклого конуса доминирования можно описать на множестве достижимых векторных оценок систему бинарных отношений в следующем виде:

, (1.17)

, (1.18)

. (1.19)

Тогда постановка задачи многокритериальной оптимизации может быть записана в виде

. (1.20)

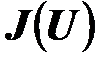Определение 1.9. Векторная оценка называется -оптимальным (оптимальным по конусу ) на множестве , если не существует , , такой, что . Соответствующее допустимое решение называется -оптимальным решением задачи (1.20). Будем обозначать множество всех -оптимальных в векторных оценок, как , а множество всех -оптимальных решений задачи (1.20), как соответственно .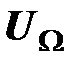

При получается отношение вида (1.14), а при - отношение вида (1.16). Это означает, что многокритериальная задача (1.12) является частным случаем задачи оптимизации по конусу (1.20), а свойства оптимальности по Парето и по Слейтеру – частными случаями оптимальности по конусу.

Конус доминирования имеет ряд полезных свойств.

Теорема 1.1 []. Пусть , - выпуклые конусы, и . Тогда в задаче (1.12)

. (1.21)

Теорема 1.2 []. Пусть , - различные выпуклые конусы. Тогда в задаче (1.12):

1) ; (1.22)

2) . (1.23)

Если конус доминирования является полиэдральным, то, как известно, его можно представить в виде системы неравенств:

, (1.24)

где - числовая матрица размерности . В этом случае взаимосвязь принципов оптимальности по конусу и оптимальности по Парето устанавливается следующей теоремой.

Теорема 1.3 (Ю) []. Пусть в задаче многокритериальной оптимизации (1.20) - полиэдральный конус доминирования вида (1.24). Рассмотрим - новый векторный показатель вида

. (1.25)

Тогда оптимальные по Парето точки для векторного показателя точно совпадают с - оптимальными точками для векторного показателя на множестве : .

Задача многокритериальной оптимизации в условиях неопределенности

Если в (1.11) отношение - замкнутый выпуклый конус доминирования, то имеет место задача многокритериальной оптимизации по конусу в условиях неопределенности:

. (1.26)

Особенность постановки (1.26) состоит в том, что каждому фиксированному решению соответствует множество , которое образуют точки в критериальном пространстве, когда вектор «пробегает» все множество . Указанную многозначность необходимо учитывать при попарном сравнении допустимых решений задачи (1.26).

Основные подходы к решению задачи (1.26), изложены в работах Гермейера, Моисеева, Куржанского А.Б., Гусева М.И., Жуковского В.И., Молоствова В.С., Салуквадзе М.Е., В.В., Р. Аумана, Б. Пелега и др., и развивают принцип гарантированного результата Гермейера Ю.Б. Согласно этому принципу оценка векторного показателя эффективности задачи (1.26) должна осуществляться по «самым плохим», иногда даже не реализующимся одновременно значениям компонентов вектора .

Определение 1.10, []. Векторная оценка называется виртуальным экстремумом относительно конуса доминирования на множестве , если она обладает следующими свойствами:

1) ; (1.27)

2) для любого такого, что , имеет место

. (1.28)

Содержательный смысл виртуального экстремума относительно конуса состоит в том, что осуществляется оценка множества по самым наихудшим относительно конуса значениям всех компонентов векторного показателя , часто даже не реализующимся одновременно. Это означает, что для любого такого, что , найдется , для которого

. (1.29)

Использование системы бинарных отношений (1.17)-(1.19) на множестве виртуальных экстремумов относительно конуса в задаче многокритериальной оптимизации по конусу в условиях неопределенности (1.26) дает возможность попарного сравнения допустимых решений .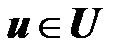

Определение 1.11. Будем говорить, что допустимое решение задачи (1.26) доминирует допустимое решение относительно конуса доминирования , если .

Таким образом, задача (1.26) с учетом отношений предпочтения (1.17)-(1.19) может быть представлена в виде детерминированной задачи многокритериальной оптимизации по конусу

, (1.30)

для решения задачи которой целесообразно применить принцип оптимальности по конусу, рассматривая в критериальном пространстве множество виртуальных экстремумов в качестве множества достижимых векторных оценок.

Определение 1.12. Допустимое решение называется оптимальным по конусу в условиях неопределенности решением задачи (1.26), если . То есть не существует , , такого, что .

При задача (1.26) превращается в (1.11), а свойство оптимальности по конусу в условиях неопределенности – в векторный минимакс [].

Определение 1.13. Векторная оценка называется виртуальным максимумом на множестве , если она обладает следующими свойствами:

1) 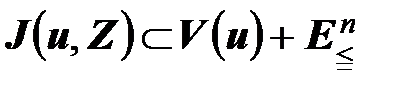; (1.31)

2) для любого такого, что , имеет место

(1.32)

Определение 1.14. Допустимое решение называется векторным минимаксом задачи (1.11), если . То есть не существует такого, что

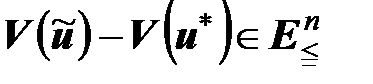. (1.33)

Задача распределенного управления с учетом внутриуровневых взаимодействий