Декартова прямоугольная система координат

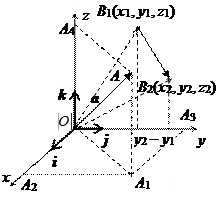Совокупность точки О (начала координат) и ортонормированного базиса i, j, k, векторы которого отложены из точки О, называется декартовой прямоугольной системой координат в пространстве. Прямые Ох, Оу, Oz, проходящие через точку О в направлении базисных ортов, называются осями координат (осью абсцисс, осью ординат, осью аппликат). Пусть А – произвольная точка пространства. Вектор r _A = ОА = x i + y j + z k называется радиусом-вектором точки А, координаты этого вектора (x, y, z) (равные проекциям вектора на координатные оси) называются также координатами точки А (обозначение: А (x, y, z)).

Расстояние между двумя точками (длина отрезка). Эту задачу мы уже рассматривали. Длина отрезка В ₁ В ₂ (верхний рисунок) равна длине вектора, соединяющего эти точки, т.е.

.

Деление отрезка в данном отношении. Говорят, что точка М делит отрезок М ₁ М ₂ в отношении , если . Найдем координаты точки М. На рисунке справа изображен отрезок и его проекция на ось Ох. Из подобия треугольников . Так же можно получить выражения для координат у, z. Окончательно, координаты точки, делящей отрезок в отношении , равны В частном случае , т.е. когда точка М – середина отрезка, получаем, что координаты середины отрезка равны средним арифметическим координат концов:

Векторное уравнение прямой. Пусть на плоскости задана точка М ₀(x ₀, у ₀) и ненулевой вектор N (A, B). В аналитической геометрии прямая задается как геометрическое место точек М (x, у) таких, что вектор 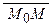ортогонален вектору N. Таким образом, в векторном виде уравнение прямой записывается так:

(скалярное произведение ортогональных векторов равно нулю).

Дальше мы вернемся к этому уравнению; сначала вспомним, что известно о прямой из школы.