Линейная зависимость и независимость системы векторов

Выражение , где коэффициенты , называется линейной комбинацией векторов а ₁, а ₂, …, а _n.

Линейная комбинация векторов называется тривиальной, если все равны нулю.

Линейная комбинация векторов называется нетривиальной, если хотя бы один из коэффициентов отличен от нуля.

Векторы а ₁, а ₂, …, а _n называются линейно независимыми, если только тривиальная линейная комбинация этих векторов равна нулевому вектору:

.

Векторы а ₁, а ₂, …, а _n называются линейно зависимыми, если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору:

.

Для линейно зависимых векторов справедливы теоремы:

Теорема Для того, чтобы векторы а ₁, а ₂, …, а _n были линейно зависимы, необходимо и достаточно, чтобы один из этих векторов был линейной комбинацией остальных.

Док-во: Необходимость. Пусть векторы а ₁, а ₂, …, а _n зависимы, т.е. существует набор чисел , из которых хотя бы одно не равно нулю, такой, что Достаточность. Пусть один из векторов есть линейная комбинация остальных, т.е. . Перепишем это равенство в виде . Мы получили нетривиальную (так как ) линейную комбинацию, равную 0, т.е. система векторов а ₁, а ₂, …, а _n действительно линейно зависима.

Теорема Если система векторов содержит линейно зависимую подсистему, то она является линейно зависимой

Теорема Любая подсистема линейно независимой системы векторов является линейно независимой.

Теорема Система векторов, содержащая нулевой вектор, является линейно зависимой.

Теорема Система векторов, содержащая два равных или два пропорциональных вектора, является линейно зависимой.

Теорема Два геометрических вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

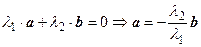Док-во. Необходимость. Пусть векторы а и b линейно зависимы. Если хотя бы один из них равен нуль-вектору, то они коллинеарны (нуль-вектор коллинеарен любому другому вектору). Если оба отличны от нуль-вектора, и существует нетривиальная линейная комбинация , равная нулевому вектору, то . Из равенства , или , где . По определению, произведение коллинеарно вектору а.

Достаточность. Пусть векторы а и b коллинеарны. Если один из них, например, а, нулевой, то нетривиальная линейная комбинация, дающая нуль-вектор, очевидна: . Если оба вектора отличны от нуль-вектора, то для равнонаправленных векторов , для противонаправленных , т.е. вектор а линейно выражается через b, что означает линейную зависимость пары векторов а и b.

Следствие. Если два вектора линейно зависимы, то один из них линейно выражается через другой.

Теорема Три геометрических вектора линейно зависимы тогда и только тогда, когда они компланарны.

Теорема Любые четыре геометрических вектора всегда линейно зависимы.

Следствие. Если векторы а, b и с некомпларны, то любой другой вектор d линейно выражается через векторы а, b и с (является их линейной комбинацией), т.е. существуют коэффициенты , и такие, что .

Базисом векторного пространства называется любая линейно независимая упорядоченная система векторов такая, что любой вектор пространства является линейной комбинацией векторов этой системы.

Разложение вектора по базису единственно (другая формулировка: равные векторы имеют равные координаты).

Док-во. Предположим, что имеется два разложения вектора а по базису е ₁, е ₂, е ₃: и . Тогда , или . Векторы базиса линейно независимы, следовательно их линейная комбинация дает нуль-вектор только в тривиальном случае: что и требовалось доказать.

Теорема. При сложении векторов их соответствующие координаты складываются.

Док-во. Пусть и . Тогда

Теорема При умножении вектора на число все его координаты умножаются на это число.

Док-во. Пусть . Тогда , что и требовалось доказать.

Линейные операции над векторами свойствами:

1. а + b = b + а;

2. (а + b) + с = а + (b + с);

3. Для любого вектора а выполняется равенство а + 0 = а.

4. Для любого вектора а существует противоположный вектор - а такой, что а + (- а) = 0.

5. 1. ;

6. ;

7. ;.

8. Для 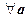выполняется равенство .

Ортогональной проекцией вектора на направление l называется число, равное длине отрезка A ₁ B ₁, где A ₁ и B ₁- основания перпендикуляров, опущенных из концов вектора на направление l, взятое со знаком плюс, если направление вектора совпадает с направлением l и со знаком минус, если направление вектора противоположно направлению l.

Проекция вектора на направление l будем обозначать .Так, на рисунке справа , .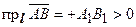

Определение скалярного произведения векторов. Скалярным произведением векторов а и b называется действительное число, равное произведению длин векторов на косинус угла 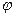между ними. Обозначения: (а, b), аb. Итак .

Свойства скалярного произведения:

1. (а, b) = (b, а);

2. (а, а) = | a |² (или (скалярный квадрат вектора равен квадрату его длины);

3. (а, b) = | b | пр _ba = | a | пр _ab;

4. (а + b, c) = (а, c) + (b, c);

5. ;

6. (а, 0) = 0;

7. если , то (а, b) = 0;

8. если (а, b) = 0, то либо хотя бы один из сомножителей равен нулю, либо сомножители ортогональны.

Док-во. Первое и второе свойства непосредственно следуют из определения: косинус – функция четная, поэтому неважно, как отсчитывается угол – от а к b или b к а; cos 0 = 1 (0 – угол, который образует вектор с самим собой). Докажем третье свойство: , или . Из этого свойства на основе свойств проекции легко выводятся четвертое и пятое:

(a + b, c) = | c | пр _c (a + b) = | c | (пр _ca + пр _cb) = | c | пр _ca + | c | пр _cb = (a, c) + (b, c),

.

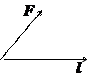Шестое, седьмое и восьмое свойства очевидны (если b = 0, то | b | = 0; если , то ; если произведение равно нулю, то необходимо один из сомножителей, входящих в определение (| a |, либо | b |, либо ) равен нулю). Если вспомнить, что мы считаем направление нуль-вектора произвольным, то восьмое свойство можно переформулировать как необходимое и достаточное условие ортогональности векторов: два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю.

Механический смысл скалярного произведения заключается в следующем. Если материальная точка под воздействием силы F перемещается на вектор l, то совершаемая этой силой работа равна скалярному произведению F на l: A = (F, l).

Базис векторного пространства называется ортонормированным, если составляющие его векторы взаимно перпендикулярны и имеют единичную длину.