Скалярное произведение векторов, заданных в ортонормированном базисе

Пусть в ортонормированном базисе i, j, k заданы векторы а = а_х i + а_у j + а_z k и b = b_х i + b_у j + b_z k. Найдем их скалярное произведение, учитывая то, что четвертое и пятое свойства позволяют раскрывать скобки и выносить скалярные множители за знак скалярного произведения и то, что вследствие ортонормированности (i, i) = (j, j) = (k, k) = 1, (i, j) = (j, i) = (i, k) = (k, i) = (j, k) =

= (k, j) = 0: (а, b) = (а_х i + а_у j + а_z k, b_х i + b_у j + b_z k) = а_х b_х (i, i) + а_х b_у (i, j) + … + а_z b_y (k, j) +

+ а_z b_z (k, k) = а_х b_х + а_y b_y + а_z b_z.

Мы доказали, что в ортонормированном базисе скалярное произведение векторов сумме попарных произведений соответствующих координат: (а, b) = а_х b_х + а_y b_y + а_z b_z.

Теперь, зная координатное представление скалярного произведения, мы можем по новому вывести формулы для длины вектора, проекции вектора на вектор и т.д. Так, (а, а) = а_х а_х + а_y а_y + + а_z а_z = а_х ²+ а_y ² + а_z ², поэтому по второму свойству | a |² = а_х ²+ а_y ² + а_z ², следовательно,

.

Из определения скалярного произведения , поэтому если векторы заданы в координатной форме, легко находится угол между ними:

.

Проекция вектора а на направление, определяемое вектором b, в координатной форме:

.

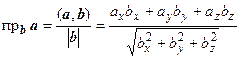В частности, если b = i = (1, 0, 0), то | b | = 1, (а, i) = (а_х i + а_у j + а_z k, 1 i + 0 j + 0 k) = а_х, и

пр _ia = а_х. Аналогично, пр _ja = а_y, пр _ka = а_z, т.е. координаты любого вектора есть проекции этого вектора на направления, заданные соответствующими ортами. Направляющие косинусы (углов между вектором а и базисными ортами i, j, k): .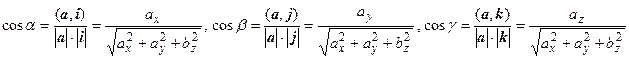

Напомним, что направляющие косинусы удовлетворяют соотношению

.

Орт вектора: .

Определение векторного произведения векторов. Векторным произведением векторов а и b называется вектор с, длина и направление которого определяются следующими условиями:

1. (или ;

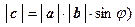2 ;

3. a, b, с - правая тройка (если векторы а и b не коллинеарны).

Обозначения: [ а, b ], .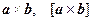

Заметим, что три условия в определении векторного определения однозначно определяют результат. Первое условие определяет длину вектора с ( так как ), второе – перпендикулярность произведения плоскости, содержащей сомножители, третье определяет нужное направление на прямой, перпендикулярной этой плоскости. Оговорка по поводу неколлинеарности сомножителей в третьем условии не сужает определение: если а и b коллинеарны, то либо по крайней мере один из этих векторов – нулевой, либо , либо ; во всех этих случаях векторное произведение дает нуль-вектор.

Свойства векторного произведения:

1. Векторное произведение антикоммутативно, т.е. [ а, b ] = - [ b, а ];

2. [ а + b, с ] = [ а, с ] + [ b, с ];

3. ;

4. [ а, b ] = 0 тогда и только тогда, когда векторы а и b коллинеарны;

5. (Геометрический смысл векторного произведения). Длина векторного произведения векторов а и b равна площади параллелограмма, построенного на этих векторах.

Док-во: 1. При изменении порядка сомножителей плоскость, в которой лежат сомножители, остается прежней, поэтому остается прежней прямая, перпендикулярная этой плоскости, однако кратчайший поворот от первого сомножителя до второго теперь виден с другой стороны, следовательно, произведение меняет знак;

1. Второе свойство будет доказано позже, после изучения свойств смешанного произведения;

2. Если , то вектор [ а, b ] растягивается (при ) или сжимается (при 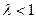) в раз; если , то [ а, b ] еще меняет и направление;

3. [ а, b ] = 0, как уже говорилось, тогда и только тогда, когда либо по крайней мере один из этих векторов – нулевой, либо , либо ; во всех этих случаях векторы коллинеарны;

4. Если на векторах а и b построить параллелограмм и рассматривать а как основание, то высота параллелограмма равна . Следствием из пятого свойства является то, что площадь треугольника, построенного на векторах а и b, равна половине длины их векторного произведения.

Упорядоченная тройка некомпланарных векторов a, b, c называется правой, если при приведении этих векторов к общему началу кратчайший поворот от a к b виден из конца вектора c против часовой стрелки (если кратчайший поворот от a к b совершается по часовой стрелке, то тройка векторов a, b, c называется левой).

Заметим, что если тройка a, b, c – правая (левая), то правыми (левыми) являются тройки b, c, a и c, a, b, т.е. ориентация не меняется при циклической перестановке векторов. В тоже время перестановка двух векторов меняет ориентацию: если тройка a, b, c – правая (левая), то тройка b, a, c (и, как следствие, тройки a, c, b и c, b, a) – левая (правая).

Ортонормированный базис в пространстве будем задавать правой тройкой ортов i, j, k. Произвольный вектор пространства a теперь может быть представлен в виде . На рисунке справа х = ОА ₂, у = ОА ₃, z = ОА ₄, все три координаты положительны. Если х, у, z – координаты вектора а в ортонормированном базисе, то (док-во: | a |² = ОА ² = ОА ₁² + A ₁ А ² (так как тр-к OAA ₁ – прямоугольный) = (ОА ₂² + A ₂ А ₁²) + A ₁ А ² = ОА ₂² + ОА ₃² + ОА ₄²).

Определение векторного произведения векторов. Векторным произведением векторов а и b называется вектор с, длина и направление которого определяются следующими условиями:

1. (или ;

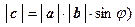2 ;

3. a, b, с - правая тройка (если векторы а и b не коллинеарны).

Обозначения: [ а, b ], .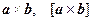

Заметим, что три условия в определении векторного определения однозначно определяют результат. Первое условие определяет длину вектора с ( так как ), второе – перпендикулярность произведения плоскости, содержащей сомножители, третье определяет нужное направление на прямой, перпендикулярной этой плоскости. Оговорка по поводу неколлинеарности сомножителей в третьем условии не сужает определение: если а и b коллинеарны, то либо по крайней мере один из этих векторов – нулевой, либо , либо ; во всех этих случаях векторное произведение дает нуль-вектор.

Свойства векторного произведения:

1. Векторное произведение антикоммутативно, т.е. [ а, b ] = - [ b, а ];

2. [ а + b, с ] = [ а, с ] + [ b, с ];

3. ;

4. [ а, b ] = 0 тогда и только тогда, когда векторы а и b коллинеарны;

5. (Геометрический смысл векторного произведения). Длина векторного произведения векторов а и b равна площади параллелограмма, построенного на этих векторах.

Док-во: 1. При изменении порядка сомножителей плоскость, в которой лежат сомножители, остается прежней, поэтому остается прежней прямая, перпендикулярная этой плоскости, однако кратчайший поворот от первого сомножителя до второго теперь виден с другой стороны, следовательно, произведение меняет знак;

1. Второе свойство будет доказано позже, после изучения свойств смешанного произведения;

2. Если , то вектор [ а, b ] растягивается (при ) или сжимается (при 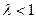) в раз; если , то [ а, b ] еще меняет и направление;

3. [ а, b ] = 0, как уже говорилось, тогда и только тогда, когда либо по крайней мере один из этих векторов – нулевой, либо , либо ; во всех этих случаях векторы коллинеарны;

4. Если на векторах а и b построить параллелограмм и рассматривать а как основание, то высота параллелограмма равна . Следствием из пятого свойства является то, что площадь треугольника, построенного на векторах а и b, равна половине длины их векторного произведения.

Механический смысл векторного произведения. Если к точке А приложена сила F, то момент этой силы относительно точки О равен .

Вычисление векторного произведения в правом ортонормированном базисе. Пусть i, j, k – базисные орты. Из картинки справа убеждаемся, что [ i, j ] = k; [ j, k ] = i; [ k, i ] = j. Кроме того, [ j, i ] = - k; [ k, j ] = - i; [ i, k ] = - j, и [ i, i ] =

=[ j, j ] = [ k, k ] = 0.

Пусть а = а_х i + а_у j + а_z k и b = b_х i + b_у j + b_z k. Тогда

[ а, b ] = [ а_х i + а_у j + а_z k, b_х i + b_у j + b_z k ] = а_х b_х [ i, i ] + а_х b_у [ i, j ] + а_х b_z [ i, k ] + … +
+ а_z b_z [ k, k ] = а_х b_у k + а_х b_z (- j) + а_у b_х (- k) + а_у b_z i + а_z b_х j + а_z b_у (- i) =

= i (а_у b_z - а_z b_у) - j (а_х b_z - а_z b_х) + k (а_х b_у - а_у b_х) = .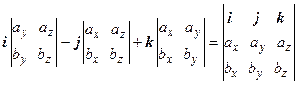

Нами доказана

Смешанным произведением векторов a, b, c называется векторно-скалярное произведение ([ a, b ], c).

Согласно этому определению первые два сомножителя умножаются векторно, затем результат скалярно умножается на третий сомножитель.

Теорема (геометрический смысл смешанного произведения). Модуль смешанного произведения векторов a, b, c равно объему параллелепипеда, построенного на этих векторах. Смешанное произведение положительно, если тройка векторов a, b, c – правая, и отрицательно, если эта тройка – левая (если векторы a, b, c компланарны, то их смешанное произведение равно нулю).

Док-во. V_пар = . Справа в этом равенстве стоит модуль смешанного произведения. Знак смешанного произведения определяется знаком косинуса: если тройка a, b, c – правая, то векторы [ a, b ] и с расположены в одном полупространстве относительно плоскости векторов a и b, , ; если тройка a, b, c – левая, то векторы [ a, b ] и с расположены в разных полупространствах относительно плоскости векторов a и b, , ; если компланарны, то высота параллелепипеда равна нулю, и V_пар =0.

Из доказанной теоремы следует, что

([ a, b ], c) = (a, [ b, c ]), так как для троек a, b, c и

b, c, а совпадают и построенные на них параллелепипеды и ориентации (циклическая перестановка). Следовательно, при сохранении порядка сомножителей не важно, где стоят квадратные скобки, обозначающие векторное произведение. Поэтому их обычно опускают, и обозначают векторное произведение просто или вообще abc.

Итак, abc = саb = bcа = – bаc = – сbа = – аcb.

Отметим еще одно очевидное следствие из теоремы. Объем треугольной пирамиды, образованной векторами a, b, c, вычисляется по формуле .