Свойства смешанного произведения

1. (а + b) cd = аcd + bcd;

2. ;

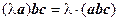3. (Необходимое и достаточное условие компланарности векторов) Смешанное произведение трёх векторов равно нулю тогда и только тогда, когда векторы компланарны;

4. Смешанное произведение не меняется при циклической перестановке сомножителей: abc = = саb = bcа;

5. Смешанное произведение меняет знак при перестановке дух сомножителей:

bаc = – аbс.

Док-во. Первые два свойства следуют из соответствующих свойств скалярного произведения (см. пункт 1.6.2 свойства 4 и 5): (а + b) cd = (а + b, [ c, d ]) = (а, [ c, d ]) + (b, [ c, d ]) =

= аcd + bcd; 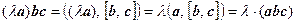; остальные свойства обсуждались выше.

Теперь мы можем доказать второе свойство векторного произведения (см. пункт .7.2. Свойства векторного произведения): [ а + b, с ] = [ а, с ] + [ b, с ]. Покажем, что векторы в левой и правой частях этого равенства имеют одинаковые координаты (тогда, по теореме 1.5.1. о единственности разложения по базису, эти векторы равны). Координаты вектора равны скалярным произведениям этого вектора на базисные орты (см. пункт 1.6.3. Скалярное произведение векторов, заданных в ортонормированном базисе). Находим эти произведения: ([ а + b, с ], i) (это смешанное произведение, для которого свойство доказано) = ([ а, с ], i) + ([ b, с ], i) = (([ а, с ] + [ b, с ]), i) – это уже произведение для суммы векторов в правой части доказываемого равенства. Так же доказываются равенства для второй (с ортом j) и третьей координат (c k).