 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Построение уравнения удобного для создания итерационного процесса
|
|
Пусть имеется уравнение 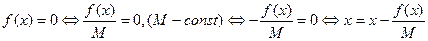 . В качестве M выбирают
. В качестве M выбирают  .
.
Итерационное уравнение будет иметь вид: 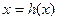 , где
, где 
Найдем  :
: 
Тогда  , если
, если 
Следовательно, в качестве  можно выбрать
можно выбрать 
Задание 4. Уточнить оставшиеся корни уравнения  методом простой итерации, предварительно приведя его к виду удобному для итераций. Погрешность 0.00001.
методом простой итерации, предварительно приведя его к виду удобному для итераций. Погрешность 0.00001.
Решение.
Приведем уравнение  к виду
к виду 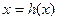 ,
,  , а
, а 
1).  -О.О.К
-О.О.К
Найдем M,  , для этого построим графики
, для этого построим графики  и
и  на этом отрезке.
на этом отрезке.
> restart;with(plots):f:=x->x^3-3*x^2-2*x+3;f1:=diff(f(x),x);


> plot(f1,x=-1.2..-1);

По графику видно, что  на
на 
> plot(abs(f1),x=-1.2..-1);
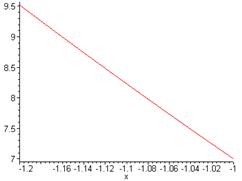
Из условий  ,
,  и графика
и графика  найдем M,
найдем M, 
> m:=7;M:=9.5; q:=1-m/M;



Запишем 
> h:=x-(x^3-3*x^2-2*x+3)/M;

Выберем начальное приближение. Например 
> x[0]:=-1;e:=.00001;
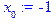

> h:=x->1.210526316*x-.1052631579*x^3+.3157894737*x^2-.3157894737;

Построим алгоритм, соответствующий формуле 
> for i from 1 by 1 to 20 do
> x[i]:=h(x[i-1]); abs(x[i]-x[i-1]);
> if abs(x[i]-x[i-1])>e*(1-q)/q then i else i:=20 end if; end do;










Таким образом корень найден  с заданной точностью 0.00001
с заданной точностью 0.00001
2)  - О.О.К
- О.О.К
Найдем M,  , для этого построим графики
, для этого построим графики  и
и  на этом отрезке.
на этом отрезке.
> plot(3*x^2-6*x-2,x=.7..0.9);

По графику видно, что  на
на 
> plot(abs(f1),x=.7...9);

Из условий  и
и  и графика
и графика  найдем M,
найдем M, 
> m:=-4.73;M:=-5;q:=1-m/M;


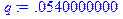
Запишем 
> h:=x-(x^3-3*x^2-2*x+3)/M;

В качестве начального приближения выберем 0,7
> x[0]:=.7;e:=.00001;


> h:=x->3/5*x+1/5*x^3-3/5*x^2+3/5;

Построим алгоритм, соответствующий формуле 
> for i from 1 by 1 to 20 do
> x[i]:=h(x[i-1]); abs(x[i]-x[i-1]);
> if abs(x[i]-x[i-1])>e*(1-q)/q then i else i:=20 end if; end do;




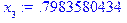

Таким образом корень найден 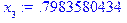 с заданной точностью 0.00001
с заданной точностью 0.00001
Дата публикования: 2015-07-22; Прочитано: 237 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
