 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Лабораторная работа № 3 Решение нелинейных уравнений
|
|
Численное решение нелинейных уравнений вида 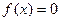 заключается в нахождении значений
заключается в нахождении значений  , удовлетворяющих с заданной точностью
, удовлетворяющих с заданной точностью 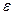 данному уравнению, и состоит из следующих основных этапов:
данному уравнению, и состоит из следующих основных этапов:
· Отделение (изоляция) корней уравнения.
· Уточнение с помощью некоторого вычислительного алгоритма конкретного выделенного корня с заданной точностью.
Целью первого этапа является нахождение области отделения корня (О.О.К.), то есть отрезка  из области определения функции
из области определения функции  , внутри которого содержится только один корень решаемого уравнения.
, внутри которого содержится только один корень решаемого уравнения.
Определение. Отрезок  из области определения функции непрерывной
из области определения функции непрерывной  будем называть областью отделения корня (О.О.К.) уравнений
будем называть областью отделения корня (О.О.К.) уравнений 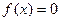 , если
, если
1)  ,
,
2)  – сохраняет знак на этом отрезке,
– сохраняет знак на этом отрезке,
3)  – сохраняет знак на этом отрезке.
– сохраняет знак на этом отрезке.
Из определения О.О.К. следует, что на отрезке  поведение функции может быть описано одним из четырех вариантов. Разберем эти варианты.
поведение функции может быть описано одним из четырех вариантов. Разберем эти варианты.

В качестве О.О.К., в этом примере можно выбрать отрезок  . Действительно, из графика видно, что
. Действительно, из графика видно, что
1)  ,
,
2)  сохраняет знак на этом отрезке
сохраняет знак на этом отрезке
3)  сохраняет знак на этом отрезке
сохраняет знак на этом отрезке

В качестве О.О.К., в этом примере можно выбрать отрезок  . Действительно, из графика видно, что
. Действительно, из графика видно, что
1)  ,
,
2)  сохраняет знак на этом отрезке
сохраняет знак на этом отрезке
3)  сохраняет знак на этом отрезке
сохраняет знак на этом отрезке

В качестве О.О.К., в этом примере можно выбрать отрезок  . Действительно, из графика видно, что
. Действительно, из графика видно, что
1)  ,
,
2)  сохраняет знак на этом отрезке
сохраняет знак на этом отрезке
3)  сохраняет знак на этом отрезке
сохраняет знак на этом отрезке

В качестве О.О.К., в этом примере можно выбрать отрезок  . Действительно, из графика видно, что
. Действительно, из графика видно, что
1)  ,
,
2)  сохраняет знак на этом отрезке
сохраняет знак на этом отрезке
3)  сохраняет знак на этом отрезке.
сохраняет знак на этом отрезке.
Других вариантов нет.
Для нахождения О.О.К. на практике используют графический или аналитический способы.
Задание 1. Используя графические возможности пакета Maple, найти отрезки отделяющие корни уравнения  .
.
Рассмотрим левую часть уравнения и построим графики функции  , ее первой и второй производных.
, ее первой и второй производных.
> restart; with(plots):
> f:=x->x^3-3*x^2-2*x+3;
> plot([f(x),diff(f(x),x),diff(f(x),x$2)],x=-1.5..4,color=[red,black,green]);


Учитывая определение О.О.К. и анализируя поведение графиков функции и ее первой и второй производных, найдем искомые отрезки.
Отрезками, отделяющими корни, являются:
 , так как
, так как
1) 
2)  сохраняет знак на этом отрезке
сохраняет знак на этом отрезке
3)  сохраняет знак на этом отрезке
сохраняет знак на этом отрезке
 , так как
, так как
1) 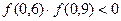 ,
,
2)  сохраняет знак на этом отрезке
сохраняет знак на этом отрезке
3)  сохраняет знак на этом отрезке
сохраняет знак на этом отрезке
 , так как
, так как
1)  ,
,
2)  сохраняет знак на этом отрезке
сохраняет знак на этом отрезке
3)  сохраняет знак на этом отрезке
сохраняет знак на этом отрезке
Таким образом, при завершении первого этапа должны быть определены промежутки, на каждом из которых содержится только один корень уравнения 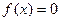 .
.
Для уточнения корней с заданной точностью 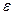 будем использовать итерационный метод, заключающийся в построении числовой последовательности
будем использовать итерационный метод, заключающийся в построении числовой последовательности 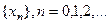 , сходящейся к искомому корню уравнения.
, сходящейся к искомому корню уравнения.
Дата публикования: 2015-07-22; Прочитано: 314 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
