Метод Ньютона (метод касательных) уточнения корней уравнения

Теорема

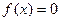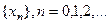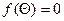Если О.О.К. уравнения и в качестве начального приближения выбран тот из концов отрезка, для которого выполняется условия , то последовательность , члены которой находятся по формуле сходиться к корню этого уравнения, т.е. , где , (Θ ).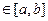

В качестве условия окончания итераций используют формулу , где и

Геометрически, метод Ньютона эквивалентен замене небольшой дуги кривой касательной, проведенной к некоторой точке кривой.

Из прямоугольного треугольника ABC

C другой стороны (AC) - касательная у графику функции в точке , тогда, из геометрического смысла производной в точке, . Таким образом , отсюда выразим :

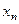Задание 2. Уточнить наибольший корень заданного уравнения методом Ньютона, с погрешностью 0.000001. Остановку процесса уточнения корня произвести в соответствии с условием , где и .

Решение.

Найдем на О.О.К.

> f:=x->x^3-3*x^2-2*x+3;f1:=diff(f(x),x);

> plot(abs(f1),x=3.2..3.4);

Из графика видно, что =9,5.

> m:=9.5;

Найдем

> f2:=diff(f(x),x$2); plot(abs(f2),x=3.2..3.4);

Из графика видно, что .=14,4

> M:=14.4;

Приступим к итерационному процессу по методу Ньютона, используя формулы

> f:=x->x^3-3*x^2-2*x+3;f1:=x->3*x^2-6*x-2;

> x[0]:=3.4;e:=0.000001;sqrt(2*m*e/M);

> for i from 1 by 1 to 20 do x[i]:=x[i-1]-f(x[i-1])/f1(x[i-1]); abs(x[i]-x[i-1]); if abs(x[i]-x[i-1])>sqrt(2*m*e/M) then i else i:=20 end if; end do;

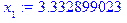
Таким образом, корень найден =3,330059 cточностью