Поверхности второго порядка

В данном параграфе приводятся канонические уравнения наиболее часто встречающихся поверхностей.

Сфера

Общее уравнение сферы радиуса с центром в точке имеет вид .

Каноническое уравнение .

Рисунок 20.

Эллипсоид

Его каноническое уравнение .

Рисунок 21.

Цилиндр

Круговой цилиндр с образующими, параллельными оси , соответствует уравнению . Если направляющей цилиндра является эллипс, его уравнение .

Рисунок 22.

Цилиндр с образующими, параллельными оси , имеет уравнение , цилиндр с осью вращения соответствует уравнению .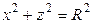

Конус

Каноническое уравнение кругового конуса с осью вращения имеет вид . Когда направляющей конуса является эллипс, его уравнение .

Рисунок 23.

Если центральная ось конуса – ось , его уравнение , если , то .

Параболоиды

Каноническое уравнение кругового параболоида с осью симметрии имеет вид , эллиптический параболоид .

Рисунок 24.

Аналогично записываются уравнения параболоидов с осями и .

Уравнения гиперболических параболоидов следующие , а также и

Рисунок 25.

Гиперболоиды

Однополостный

Уравнение кругового гиперболоида с осью симметрии имеет вид , эллиптического

Рисунок 26.

Однополостный гиперболоид имеет центральную ось , гиперболоид имеет центральную ось .

Двухполостные гиперболоиды имеют уравнения , , .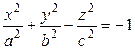

Рисунок 27.