 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Прямая и плоскость
|
|
В этой теме решаются смешанные задачи геометрии в пространстве.
Угол между прямой и плоскостью
Если обозначить угол между прямой и плоскостью 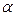 , а угол между нормальным вектором плоскости и направляющим вектором прямой
, а угол между нормальным вектором плоскости и направляющим вектором прямой 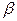 , очевидно, имеет место связь
, очевидно, имеет место связь 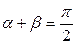 .
.
Имея уравнение плоскости 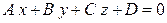 и прямой
и прямой 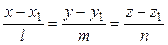 , получаем
, получаем 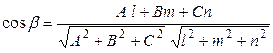 , откуда следует формула для угла между прямой и плоскостью
, откуда следует формула для угла между прямой и плоскостью
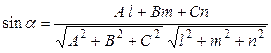 .
.
Отсюда следует условие параллельности прямой и плоскости
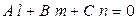 ,
,
и условие их перпендикулярности
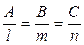 .
.
Пересечение прямой с плоскостью
Для решения этой задачи можно использовать общие уравнения прямой
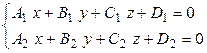 и плоскости
и плоскости 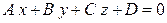 , тогда задача сводится к решению системы трех уравнений
, тогда задача сводится к решению системы трех уравнений
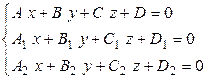 .
.
Можно решить задачу проще, задав прямую параметрически. Имеем
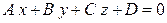 и
и 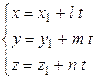 . Подставляем
. Подставляем  из уравнения прямой в уравнение плоскости и получаем одно уравнение относительно параметра
из уравнения прямой в уравнение плоскости и получаем одно уравнение относительно параметра 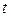 . Это уравнение может иметь единственное решение, тогда подставляя в уравнение прямой найденное значение параметра, определяем точку пересечения. Уравнение может не иметь решения, тогда прямая параллельна плоскости, наконец, уравнение может иметь бесчисленное множество решений, тогда прямая лежит в плоскости.
. Это уравнение может иметь единственное решение, тогда подставляя в уравнение прямой найденное значение параметра, определяем точку пересечения. Уравнение может не иметь решения, тогда прямая параллельна плоскости, наконец, уравнение может иметь бесчисленное множество решений, тогда прямая лежит в плоскости.
Примеры.
1. Определить общие точки прямой и плоскости
а) 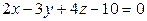 ,
, 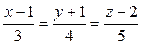 .
.
Приведем уравнение прямой к параметрическому виду
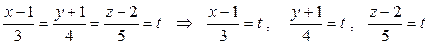
откуда следует 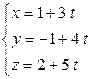 . Подставляем эти соотношения в уравнение плоскости
. Подставляем эти соотношения в уравнение плоскости 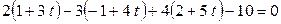 . Тогда
. Тогда 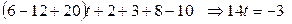 ,
, 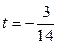 , и точка пересечения имеет координаты
, и точка пересечения имеет координаты 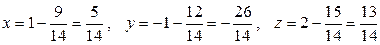 .
.
Ответ 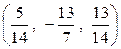 .
.
в) 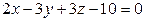 ,
, 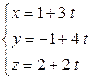 .
.
Решение. 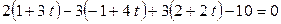 , откуда следует
, откуда следует
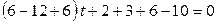 или
или 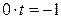 . Уравнение не имеет решения. Проверим условие параллельности прямой с плоскостью
. Уравнение не имеет решения. Проверим условие параллельности прямой с плоскостью 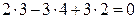 .
.
Действительно, прямая параллельна плоскости, следовательно, не имеет с ней общих точек.
с) 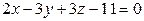 ,
, 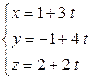 .
.
Решение.
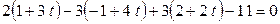 ,
,
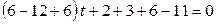 откуда следует
откуда следует 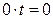 , и уравнение имеет решение при любых
, и уравнение имеет решение при любых 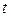 . Прямая лежит в плоскости.
. Прямая лежит в плоскости.
2. Определить угол между прямыми. Пусть прямые заданы следующими уравнениями 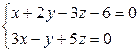 ,
, 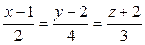 . Направляющий вектор второй прямой
. Направляющий вектор второй прямой 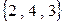 . Направляющий вектор первой прямой определим следующим образом. Нормальные векторы обеих плоскостей, определяющих прямую, ортогональны своим плоскостям. Направляющий вектор прямой лежит как в одной, так и в другой плоскости, следовательно, он ортогонален нормальным векторам обеих плоскостей. Очевидно, его можно определить как векторное произведение нормальных векторов, то есть
. Направляющий вектор первой прямой определим следующим образом. Нормальные векторы обеих плоскостей, определяющих прямую, ортогональны своим плоскостям. Направляющий вектор прямой лежит как в одной, так и в другой плоскости, следовательно, он ортогонален нормальным векторам обеих плоскостей. Очевидно, его можно определить как векторное произведение нормальных векторов, то есть
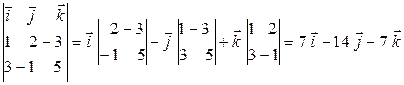 ,
,
или 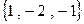 , поскольку длина направляющего вектора в этом случае несущественна.
, поскольку длина направляющего вектора в этом случае несущественна.
Угол между прямыми определяется по формуле
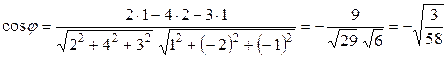 .
.
Примеры для самоподготовки.
1. Через точу 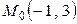 провести прямую, перпендикулярную плоскости
провести прямую, перпендикулярную плоскости  .
.
2. Записать уравнение плоскости, проходящей через точку 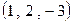 перпендикулярно прямой
перпендикулярно прямой 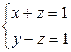 .
.
3. Записать уравнение плоскости, проходящей через параллельные прямые 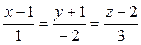 и
и 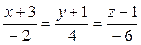 .
.
Дата публикования: 2015-07-22; Прочитано: 383 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
