 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Деление отрезка в заданном отношении
|
|
Дан отрезок 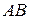 , причем
, причем 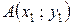 и
и 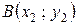 . Определить координаты
. Определить координаты
точки 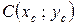 , делящей отрезок в отношении
, делящей отрезок в отношении 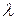 . Очевидно,
. Очевидно, 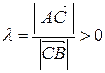 .
.
Если векторы 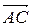 и
и 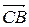 сонаправлены (
сонаправлены (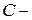 внутренняя точка отрезка), то последнее соотношение можно представить в векторной форме
внутренняя точка отрезка), то последнее соотношение можно представить в векторной форме 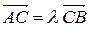 , и поскольку
, и поскольку  , получаем векторное уравнение
, получаем векторное уравнение
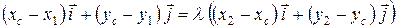 .
.
Известно, что два вектора равны, если равны их соответствующие проекции, отсюда следует
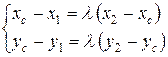 .
.
Из этой системы уравнений определяем искомые координаты точки 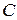 :
:
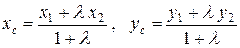 .
.
Замечание 1. В полученных формулах существенно, какая точка отрезка считается первой, и какая второй. В самом деле, если 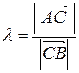 , то
, то 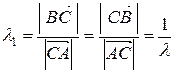 . Другими словами, одна и та же точка
. Другими словами, одна и та же точка 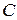 делит отрезки
делит отрезки 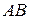 и
и 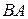 в различном отношении.
в различном отношении.
Замечание 2. Если за основное принять векторное равенство 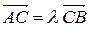 , точка
, точка 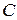 может находиться вне отрезка
может находиться вне отрезка 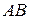 , тогда векторы
, тогда векторы 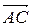 и
и 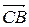 противоположно направлены, полученные формулы при этом справедливы, но
противоположно направлены, полученные формулы при этом справедливы, но 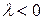 .
.
При 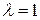 имеем известные их школы формулы координат середины отрезка
имеем известные их школы формулы координат середины отрезка 
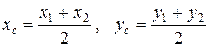 .
.
Дата публикования: 2015-07-22; Прочитано: 1111 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
