Расчёт параметров зацепления

Для достаточно узких зубчатых колёс коробок передач достаточным является условие, при котором коэффициент осевого перекрытия ε_β = 1. Угол наклона β ¹, удовлетворяющий условию ε_β = 1, будет равен:

β ¹ = arcsin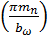

Сразу его вычислим:

β ¹ = arcsin = 35,6 град

Суммарное приведённое число зубьев z _{∑ пр} определяют по формуле:

z _{∑ пр} = z ₁ + z ₂ =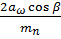

Определим их:

z _{∑ пр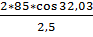} = = 59,57 =60

z _{∑ пр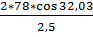} = = 54,2 = 54

По найденным значениям чисел зубьев шестерни и колеса уточняют передаточное число зацепления u_i. По полученным значениям уточняют межосевое расстояние а_ω, значение которого должно быть не менее a_ω(Н,F):

а_ω = 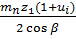≥ a_ω(Н,F)

Посчитаем и получим:

а_ω = 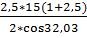= 77,2 ≥ a_ω(Н,F)

Определим количество зубьев с корекцией:

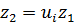= 2,5*17 = 38

После этого корректируют угол наклона зуба β:

β = arccos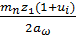

Определим:

β = arccos 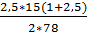= 36,35 град

Выбранное наибóльшее значение межосевого расстояния а_ω определяют с учётом изменения угла зацепления (из – за смещения исходного контура) по формуле:

а_ω =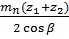

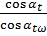
где	z 1 и z 2 – числа зубьев шестерни и колеса соответственно; αt – делительный угол зацепления в торцовом сечении, град; αtω – угол зацепления в торцовом сечении зубчатого зацепления, выполненного со смещением исходного контура, град.

Определим его:

а_ω = = 78,74 мм

Определим делительный d и начальный d_ω диаметры шестерни и колеса:

d_ω = d1= 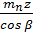= = 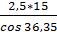44,57 мм

d_ω = d2= 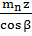= =113 мм

9. Расчёт геометрических параметров зубчатых передач

При определении геометрических параметров зубчатых передач КП общими исходными данными для всех зацеплений являются:

- межосевое расстояние а_{ω =} 78, мм;

- нормальный модуль зацепления m_{n =} 2,5 мм;

- суммарное число зубьев z_{∑ =} 54

- угол наклона зубьев колёс β = 36,35 град.