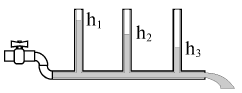
Рассмотрим течение вязкой жидкости, обратившись непосредственно к опыту. Подключим тонкую горизонтальную стеклянную трубу с впаянными в нее вертикальными манометрическими трубками при помощи резинового шланга к водопроводному крану (рис. 4.6).
|
| Рис. 4.6.
|
При небольшой скорости течения воды легко усматривается понижение уровня воды в манометрических трубках в направлении течения (h1>h2>h3). Это в свою очередь указывает на наличие горизонтального градиента давления - статическое давление жидкости уменьшается вдоль потока. При равномерном прямолинейном течении жидкости силы давления уравновешиваются силами вязкости, а силы инерции отсутствуют вовсе. Уравнение Навье-Стокса для этого случая запишется в виде
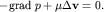
| (4.12)
|
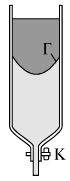
Распределение скоростей в поперечном сечении потока вязкой жидкости можно наблюдать при ее вытекании из вертикальной трубки через узкое отверстие (рис. 4.7).
|
| Рис. 4.7.
|
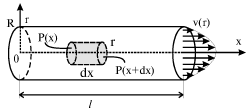
Если, например, при закрытом кране К налить вначале подкрашенный сахарный сироп, а затем поверх осторожно налить неподкрашенный сироп, то в состоянии равновесия граница раздела Г будет горизонтальной. Если кран К открыть, то граница раздела примет форму, похожую на параболоид вращения. Это указывает на существование распределения скоростей в сечении трубки при вязком течении сиропа. Нетрудно вычислить это распределение скоростей потока в поперечном его сечении. Это можно сделать, записав уравнение (4.12) в цилиндрических координатах (x, r) и проинтегрировав его. Однако мы поступим несколько проще, если приравняем силы вязкости и давления, действующие на цилиндрический объем жидкости радиуса r и длиной dx (рис. 4.8):
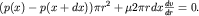
| (4.13)
|
Отметим, что равнодействующая сил давления направлена по потоку (вдоль оси x), а сила вязкого трения, приложенная к боковой поверхности цилиндрического объема - против потока, поскольку dv/dr<0. Произведя сокращение и разделив (4.13) на dx, получаем
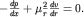
| (4.14)
|
Величина градиента давления dp/dx в (4.14) не зависит от радиуса r, т.к. давление p=p(x) и в поперечном сечении x=const не меняется. Это позволяет проинтегрировать (4.14) по радиусу:
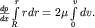
| (4.15)
|
Уравнение (4.15) позволяет рассчитать распределение скоростей, при условии, что у стенок трубы эта скорость равна нулю. После интегрирования (4.15) получаем
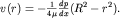
| (4.16)
|
Давление равномерно падает в направлении оси x, поэтому dp/dx<0 и не зависит от x. Параболическое распределение скоростей (4.16) графически изображено на рис. 4.8 у выходного сечения трубы. Поток вектора скорости через поперечное сечение трубы, или жидкости, протекающей через сечение в единицу времени (на практике употребляют термин "расход жидкости") оказывается равным
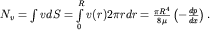
| (4.17)
|
Для практических целей расход жидкости определяют по формуле Пуазейля
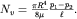
| (4.18)
|
Здесь расход воды Nv пропорционален разности давлений p1-p2 на концах трубы длиной  . Следует обратить внимание на существенную зависимость пропускной способности трубы от ее радиуса R. При заданном давлении на входе водопроводной сети увеличение диаметра труб вдвое влечет увеличение их пропускной способности в 16 раз!
. Следует обратить внимание на существенную зависимость пропускной способности трубы от ее радиуса R. При заданном давлении на входе водопроводной сети увеличение диаметра труб вдвое влечет увеличение их пропускной способности в 16 раз!
|
| Рис. 4.8.
|
Пользуясь формулой Пуазейля можно определить вязкость жидкости. Так, например, в опыте, изображенном на рис. 4.6, легко измерить разность давлений и расход жидкости и при известном радиусе горизонтальной трубки посчитать вязкость жидкости Однако более удобно вязкость жидкости определять по методу Стокса, измеряя время падения шарика в этой жидкости (см. ниже).
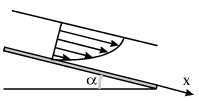
Параболический профиль скорости слоев, как нетрудно подсчитать, будет и при течении жидкости между двумя пластинами (рис. 4.4). Если этот рисунок разрезать посередине на высоте и наклонить нижнюю пластину под углом  , то мы получим картину слоистого течения воды в реке под действием силы тяжести (рис. 4.9). Вместо перепада давления dp/dx мы можем использовать компоненту силы тяжести
, то мы получим картину слоистого течения воды в реке под действием силы тяжести (рис. 4.9). Вместо перепада давления dp/dx мы можем использовать компоненту силы тяжести 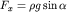 при расчете профиля скоростей течения.
при расчете профиля скоростей течения.
|
| Рис. 4.9.
|


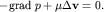

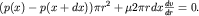
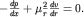
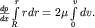
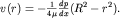
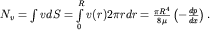
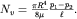
 . Следует обратить внимание на существенную зависимость пропускной способности трубы от ее радиуса R. При заданном давлении на входе водопроводной сети увеличение диаметра труб вдвое влечет увеличение их пропускной способности в 16 раз!
. Следует обратить внимание на существенную зависимость пропускной способности трубы от ее радиуса R. При заданном давлении на входе водопроводной сети увеличение диаметра труб вдвое влечет увеличение их пропускной способности в 16 раз!
 , то мы получим картину слоистого течения воды в реке под действием силы тяжести (рис. 4.9). Вместо перепада давления dp/dx мы можем использовать компоненту силы тяжести
, то мы получим картину слоистого течения воды в реке под действием силы тяжести (рис. 4.9). Вместо перепада давления dp/dx мы можем использовать компоненту силы тяжести 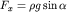 при расчете профиля скоростей течения.
при расчете профиля скоростей течения.
