 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Основная теорема зацепления
|
|
Вывод теоремы и ее формулировка определяют условие, которому должны отвечать боковые профили зубьев, находящихся друг с другом в зацеплении.
Рассмотрим картину касания двух боковых профилей зубьев. Пусть эти профили будут очерчены какими-то кривыми (рис. 5.6), касающимися друг друга в точке М.

Рис. 5.6. Картина зацепления двух соприкасающихся боковых профилей
Прямая n-n является общей нормалью к этим кривым. Представим вращение профилей зубьев вокруг осей О1 и О2 с угловыми скоростями ω1 и ω2. Тогда векторы окружных скоростей  и
и  точек M1 и M2, принадлежащих этим профилям, будут направлены перпендикулярно радиусам О1M и O2M, а их величины
точек M1 и M2, принадлежащих этим профилям, будут направлены перпендикулярно радиусам О1M и O2M, а их величины
 ,
,
 .
.
Спроектируем эти скорости на нормаль n-n и получим векторы  и
и  .
.
Для соблюдения нормальной работы зацепления необходимо обеспечить равенство этих векторов:
 .
.
В противном случае будет или «убегание» левого профиля (если  ), или «набегание» правого на левый (
), или «набегание» правого на левый (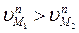 ), что в принципе невозможно.
), что в принципе невозможно.
Рассмотрим подобие треугольников:
 .
.
Из свойства соотношения сторон составим уравнение пропорции
 ,
,
откуда
 .
.
Из аналогичного подобия  и
и  получим
получим
 .
.
Так как  , то
, то
 ,
,
или
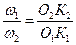 . (5.1)
. (5.1)
|
 , тогда
, тогда  , а уравнение (5.1) запишем в виде
, а уравнение (5.1) запишем в виде
Это и есть основная теорема зацепления: нормаль n-n к профилям, образующим высшую кинематическую пару, проведенная к точке их касания, делит межосевые расстояния  на отрезки, обратно пропорциональные угловым скоростям, с которыми эти профили вращаются.
на отрезки, обратно пропорциональные угловым скоростям, с которыми эти профили вращаются.
Дата публикования: 2015-07-22; Прочитано: 549 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!

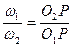 .
.