Тема 1. Прямая линия на плоскости

ГЛАВА II. Элементы векторной алгебры и аналитической геометрии.

Тема 1. Прямая линия на плоскости.

Одной из важных задач в математике является задача определения положения точки. Эта задача решается разными способами. Один способ хорошо известен из школьной программы. Это определение положения точки с помощью декартовой системы координат.

Для этого на плоскости фиксируются две взаимно перпендикулярные числовые оси. Горизонтальная ось -ось абсцисс и вертикальная ось -ось ординат. Точка пересечения О этих осей называется началом координат. Плоскость, на которой введена система координат, называется координатной плоскостью.

У1

Х1

M

На координатной плоскости возьмем произвольную точку и проведём через неё прямые параллельные координатным осям. Пересечение прямой с осью даёт нам единственное число 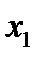, а пересечение прямой с осью даёт нам единственное число .

Обратно, если задана пара чисел 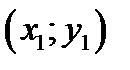, ,то из рис.1 видно, что она определяет единственную точку .

рис.1

Определение 1.1. Упорядоченная пара чисел 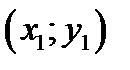, определяющая положение точки на координатной плоскости называется прямоугольными декартовыми координатами точки. Число 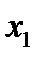называют абсциссой точки, а число ординатой точки . Произвольную точку на координатной плоскости будем обозначать так . Каждая точка имеет свои координаты и наоборот каждая пара координат задаёт одну определённую точку. Каждое правило теперь может быть сформулировано на двух разных языках: 1) на геометрическом языке и 2)на аналитическом языке (языке координат)

Например, задать точку на координатной плоскости это значит: 1)либо обозначить её на плоскости, 2) либо задать её координаты. Найти точку это значит: 1) либо найти её положение на координатной плоскости, 2) либо найти её координаты. Если задавать абсциссу и ординату точки независимо друг от друга, то на координатной плоскости получим совершенно произвольные расположения точек . Если же координаты и 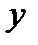связаны между собой определённым правилом, то меняя их по этому правилу, получаем на плоскости кривую, состоящую из этих точек.

Например, если сумма квадратов координат равна 1

, то получаем окружность радиуса 1. На практике различные расчёты с геометрическими объектами производятся в координатах. Затем, если это нужно, полученные результаты переводятся для наглядности на геометрический язык. На языке координат задать линию значит задать правило связывающее между собой ординату 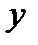и абсциссу . Такое правило называется уравнением линии в координатной плоскости. Мы начнём изучение линий на координатной плоскости с наиболее простой прямой линии, которая, тем не менее, играет одну из самых важных ролей в математике.