Преобразование Фурье

Наиболее простой периодический сигнал – синусоидальная волна. В общем случае такую волну можно задать тремя параметрами – максимальной амплитудой А, частотой f и фазой 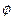. Максимальной амплитудой называется максимальное значение или интенсивность сигнала во времени (измеряется в вольтах). Частотой называется темп(в периодах за секунду - 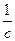или герцах - Гц) повторения сигнала. Фаза является мерой относительного сдвига по времени в пределах одного периода сигнала. Ее можно определить как часть дробного отношения , где Т – период, а t – время, отсчитываемое от произвольного начала отсчета. За начало отсчета обычно принимается последнее предыдущее прохождение ин6тенсивности сигнала через ноль от отрицательного значения к положительному.

В общем случае синусоидальный сигнал можно представить в виде . Эффект изменения каждого из трех параметров показан на рисунке 2.1. По горизонтальной оси рисунка 2.1 откладывается время. На самом же графике показана зависимость от времени величины сигнала в данной точке пространства. Такие же графики, при изменении масштаба, можно получить, если отложить на горизонтальной оси расстояние. В этом случае на графике будет изображена величина сигнала в данный момент времени в зависимости от расстояния. Например, при передаче синусоидальной волны (если рассмотреть электромагнитную радиоволну на некотором расстоянии от радиоантенны или звук на некотором расстоянии от громкоговорителя) в отдельный момент времени интенсивность сигнала меняется по гармоническому закону как функция расстояния от источника.

а) А=1; f=1; 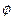=0 б) А=0,5; f=1; 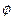=0

в) А=1; f=2; 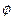=0 г) А=0,5; f=1; =

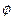Рисунок 2.1 Синусоидальный сигнал

Для синусоидальных сигналов существует два простых соотношения, одно из которых связано со временем, а другое – с пространством. Определим длину волны как расстояние, занимаемое одним периодом или, иными словами, как расстояние между двумя точками равных фаз двух последовательных циклов. Предположим, что сигнал распространяется со скоростью v. Тогда длина волны связана с периодом следующим соотношением:

или равносильно (2.10)

Важным частным случаем этого соотношения является случай м/с

где с – скорость света в вакууме.

Реальный электромагнитный сигнал состоит из многих частот. Рассмотрим сигнал, представленный на рисунке 2.2, аналитически записываемый в виде . Составляющими этого сигнала являются простые синусоидальные сигналы с частотами f и 3f. Отметим несколько особенностей:

· Вторая частота кратная первой. Если частотные составляющие сигнала кратны одной частоте, то эта частота называется собственной частотой.

· Период суммарного сигнала равен периоду сигнала собственной частоты.

Можно показать, использовав для этой цели методик, известную как анализ Фурье, что любой сигнал можно разложить на гармоники различных частот. Этот факт имеет большое значение в теории связи, так как воздействие на сигнал различных передающих сред можно выразить в терминах частот.

а)

б)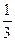

в)

Рисунок 2.2 Сложение гармоник

Для каждого сигнала существует функция времени s(t), задающая амплитуду сигнала в каждый момент времени. Подобным образом существует функция частоты S(f), задающая максимальную амплитуду гармоник, составляющих сигнал. На рисунке 2.3 показана частотная функция для сигнала, приведенного на рисунке 2.2,в. В этом случае функция S(f) дискретна. На рисунке 2.4 показана частотная функция для отдельного прямоугольного импульса, имеющего значение 1 в области от –X/2 до X/2 и 0 в остальной области. В этом случае функция S(f) непрерывна и принимает неограниченное число ненулевых значений, хотя амплитуда частотных компонент быстро уменьшается с ростом f.

Рисунок 2.3 Спектр гармонического сигнала

Рисунок 2.4 Спектр прямоугольного импульса

Если в сигнале имеется гармоника нулевой частоты, она называется постоянной составляющей. Если постоянной составляющей нет, средняя амплитуда сигнала равна нулю. На рисунке 2.5 показан результат добавления постоянной составляющей к сигналу, изображенному на рисунке 2.2,в.

а)

б) S(f)

Рисунок 2.5 Сигнал с постоянной составляющей

Спектром сигнала называется диапазон частот, составляющих данный сигнал. Для сигнала, приведенного на рисунке 2.2,в спектр лежит в области от f до 3f.

Периодический сигнал g(t) c периодом Т в общем случае имеет бесконечный спектр, который можно выразить в виде ряда Фурье:

(2.11)

где - круговая частота

- постоянная составляющая сигнала, которая может отсутствовать

и - гармоники основной частоты

и - вторые гармоники

Ряд (2.11) можно записать в более компактной форме:

(2.12)

Пары коэффициентов и вместе со своими косинусными и синусными множителями являются ни чем иным, как представлением одиночного вращающегося вектора в полярной системе координат (см. рисунок 2.6). Амплитуда этого вектора равна , а его угловая скорость рад/с. Каждый вектор в момент времени t=0 имеет произвольную фазу, которая вычисляется по формуле:

(2.13)

Амплитуда равна

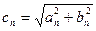(2.14)

Рисунок 2.6 Графическое представление гармоники

Формулу (2.12) можно также переписать в виде:

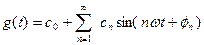(2.15)

Между сигналом s(t) и его спектром S() существует однозначное соответствие. Для практических приложений важно установить связь между преобразованием сигнала и соответствующим ему преобразованием спектра.

1. Если сигнал запаздывает во времени, амплитуда его частотного спектра не меняется, а фазовый спектр сдвигается по фазе.
2. Умножение произвольного сигнала на синусоиду частоты f₀ приводит к трансляции исходного спектра сигнала на f₀ и - f₀ (теорема о модуляции (смешивании))
3. При сжатии сигнала в n раз по временной оси во столько же раз расширяется его спектр на оси частот. Модуль спектральной плотности при этом уменьшается в n раз. При растягивании сигнала во времени спектр сужается и увеличивается модуль спектральной плотности.

Абсолютной шириной полосы сигнала называется ширина его спектра. На рисунке 2.3 ширина полосы сигнала равна 2f. Ширина полосы сигнала, спектр которого представлен на рисунке 2.4, бесконечна. Но большая часть энергии сигнала приходится на относительно узкую полос частот, называемую эффективной полосой.