Основне рівняння молекулярно-кінетичної теорії ідеального газу

· Тиск газу в молекулярно-кінетичній теорії

· Виведення основного рівняння молекулярно-кінетичної теорії ідеального газу

· Парціальний тиск

Тиск газу в молекулярно-кінетичній теорії. Тиск газу на оточуючі тіла – найголовніша відмінність газу від рідин і твердих тіл. З курсу фізики 8 класу ви знаєте, що тиск газу на стінки посудини (чи будь-яку іншу поверхню) зумовлений ударами молекул. Молекули газу стикаючись із будь-якими перепонами на їх шляху (стінки посудини, люди, тварини, автомобілі, скелі), діють на них. У результаті удару, наприклад об стінку посудини, кожна молекула передає їй імпульс, а отже, діє на неї з певною (дуже малою) силою. Натомість стінка діє на молекулу з такою самою силою у протилежному напрямі. Коли кількість молекул у посудині мала, ці удари відбуваються зі значними (у молекулярному масштабі) інтервалами часу, і це сприймається не як безперервна дія, а як низка послідовних дуже малих дій. Коли кількість молекул у посудині велика, що реально (крім штучно створюваних умов високого вакууму), ці удари відбуватимуться безперервно. Нескінченно малі дії окремих молекул додаються і результуюча дія сприймається як практично постійно діюча сила.

Таким чином, згідно з молекулярно-кінетичними уявленнями тиск газу виникає в результаті ударів молекул об стінки посудини.

Тиск газу (р) - усереднена за часом результуюча сила дії молекул на одиницю площі посудини.

Це величина, яка характеризує стан великої кількості молекул, тобто макроскопічна величина. У випадку однієї чи кількох молекул поняття тиску взагалі втрачає сенс.

За одиницю тиску в СІ беруть такий тиск, за якого на 1 м² поверхні на неї діє сила в 1 Н. Цю одиницю називають паскалем: 1 Па = 1 Н/м².

Використовують і позасистемні одиниці: міліметр ртутного стовпчика (1 мм рт.ст.≈133,3 Па); атмосфера (1 атм≈10⁵ Па).

Вимірюють тиск газу нижчий і вищий від атмосферного за допомогою манометрів, атмосферний – барометрами.

Оскільки величезна кількість молекул газу рухається хаотично, то відбувається у середньому однакова кількість ударів у будь-якому напрямі, а отже, тиск на всі стінки посудини має бути однаковим, на що вказує закон Паскаля.

Виведення основного рівняння молекулярно-кінетичної теорії ідеального газу. Використовуючи модель ідеального газу, німецький фізик Рудольф Клаузіус вивів рівняння, що встановлює зв’язок між тиском ідеального газу p, масою молекули m₀, концентрацією молекул n і середнім квадратом швидкості .

Рудольф Клаузіус

Точне виведення рівняння молекулярно-кінетичної теорії досить складне, зрозуміти його і запам’ятати нелегко. Доказ майже кожного твердження у фізиці, виведення будь-якого рівняння можна виконати з різним ступенем точності і переконливості: дуже спрощено, більш-менш точно і з великою точністю, доступною сучасному стану розвитку науки. Ми обмежимось дуже спрощеним, схематичним виведенням рівняння.

Нехай всередині посудини, площа стінки якої S міститься ідеальний одноатомний газ з молекулами масою кожна, які хаотично рухаються. Згідно статистичних закономірностей можна вважати, що кожна молекула має одну й ту саму швидкість, значення якої відповідає середній квадратичній швидкості руху сукупності молекул

.

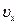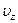Як відомо, вектор швидкості має три складові , , вздовж взаємно перпендикулярних осей Oх, Oу, Oz у декартовій системі координат (мал. 12).

Мал. 12. Проекції вектора швидкості на осі системи координат

Квадрат вектора швидкості пов’язаний з його компонентами таким співвідношенням: .

Таке ж співвідношення справедливе і для середнього квадрату швидкості: .

Повна хаотичність руху дозволяє стверджувати, що рух за всіма напрямами відбувається з однаковою швидкістю, тому , а отже , звідки

.

Припустімо, що молекули газу рухаються від однієї стінки до іншої без взаємних зіткнень. Це спрощення внаслідок великої кількості молекул і хаотичності їх руху не впливає на точність розрахунків. Під час зіткнення зі стінками посудини молекули ідеального газу взаємодіють з ними за законами механіки як абсолютно пружні тіла. Молекула діє на стінку із силою 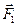, що дорівнює за третім законом Ньютона силі , з якою стінка посудини діє на молекулу і протилежна їй за напрямом.

Нехай молекула масою рухається зі швидкістю в напрямі стінки посудини, площа якої (мал. 13).

Мал. 13. Пружний удар молекули об стінку посудини у виділеному об’ємі

Пружно вдарившись об стінку, вона передає їй імпульс: . Оскільки взаємодія пружна, тобто модуль швидкості не змінюється, а напрям руху змінюється на протилежний , то .

Якщо швидкість руху молекули направлена під довільним кутом до стінки, то під час зіткнення молекули із стінкою проекція її швидкості на напрям, перпендикулярний до поверхні стінки, змінює знак , а проекції швидкостей та на напрями, паралельні поверхні стінки лишаються без змін. Таким чином зміна проекції імпульсу молекули дорівнює: .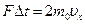

Щоб обчислити імпульс сили, що діє на стінку з боку молекул, необхідно підрахувати кількість зіткнень молекул із стінкою за час .

За час стінки посудини можуть досягти лише ті молекули, які знаходяться в об’ємі:

.

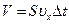Оскільки в цьому об’ємі половина молекул рухається до стінки, а половина від неї, то кількість молекул , які вдаряться об стінку за час , буде дорівнювати:

,

де – концентрація молекул.

Підставивши значення об’єму отримаємо:

.

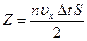Усі ці молекули передадуть стінці імпульс, що згідно з другим законом Ньютона дорівнює імпульсу сили:

або з урахуванням попереднього виразу .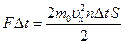

Після спрощень, сила , з якою діють молекули на стінку площею , дорівнює:

.

Оскільки швидкості молекул різні, і кожна з них, ударяючись об стінку вносить свій особливий вклад у тиск, то беруть середнє за всіма молекулами значення квадрата проекції швидкості .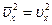

Врахувавши, що , а тиск , то одержимо вираз основного рівняння молекулярно-кінетичної теорії газів:

.

Основне рівняння МКТ газів установлює зв’язок між тиском (макроскопічним параметром) з такими мікроскопічними параметрами, як маса однієї молекули і середня квадратична швидкість руху молекул. Дає можливість, знаючи масу молекули , визначити середню квадратичну швидкість і концентрацію молекул , розрахувати тиск, який чинить газ на стінку посудини, в якій він знаходиться.

Це рівняння можна подати і в іншому вигляді. Поділимо і помножимо праву частину рівняння на 2: .

Звідси можна зробити важливий висновок: тиск ідеального газу пропорційний середній кінетичній енергії хаотичного руху молекул.

Або, врахувавши, що 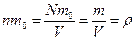, отримуємо: .

Основне рівняння МКТ газів підтверджує той факт, що чим більша маса молекул і їх швидкості, а також концентрація, тим більший тиск вони чинять на стінки посудини.

Це рівняння – перше кількісне співвідношення, добуте в молекулярно-кінеимчній теорії, тому його називають основним. Після виведення цього рівняння в середині ХІХ ст. й експериментального доведення його справедливості розпочався швидкий розвиток кількісної молекулярно-кінетичної теорії, який триває і досі.

Парціальний тиск. Якщо газ складається із суміші ідеальних газів, молекули кожного газу ударяють об стінку посудини незалежно одна від одної.

Парціальний тиск – це тиск, що його чинив би газ, який входить до складу суміші газів, коли б один при даній температурі займав увесь об'єм.

Відповідно до принципу суперпозиції сил, тиски газів, які складають суміш (парціальні тиски), додаються. Це твердження вперше сформулював у 1801 р. англійський фізик і хімік Д. Дальтон (1766 – 1844), тому його називають законом Дальтона.

Закон Дальтона: тиск суміші газів дорівнює сумі парціальних тисків складових газів:

р = р₁ + р₂ +... +р_п.

Строго виконується для суміші ідеальних газів; наближе­но застосовується для реальних газів при певних значеннях тем­ператур і тисків (далеких від критичних). Так, атмосферний тиск складається із парціальних тисків азоту, кисню та інших газів.

Джон Дальтон (1766-1844)

Дайте відповіді на запитання

1. Який механізм виникнення тиску газу з погляду МКТ?

2. Виведіть і поясніть фізичний зміст основного рівняння МКТ.

3. Які особливості основного рівняння ідеального газу і чому його називають основним?

4. Які існують інші форми запису основного рівняння МКТ газів? Що таке парціальний тиск? У чому полягає суть закону Дальтона?