Застосування векторного добутку

За допомогою векторного добутку можна скласти рівняння площини, яка проходить через три задані точки. Нехай задано три точки:

.

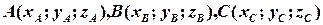За нормальний вектор 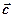шуканої площини можна взяти векторний добуток 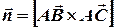. Отже, рівняння площини буде мати вигляд:

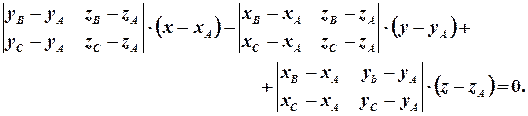
При цьому три точки однозначно визначають площину в просторі, коли вони не лежать на одній прямій, а це, у свою чергу, еквівалентно не колінеарності відповідних векторів 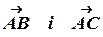. Для цього за критерієм колінеарності двох векторів (див. п.5.2) необхідно і достатньо, щоб виконувалась нерівність 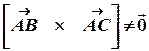, тобто, щоб одночасно виконувались нерівності:

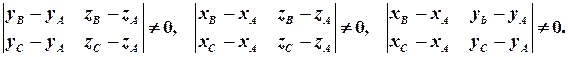
Ще одне застосування векторного добутку, яке так само випливає з його означення, – це обчислення площі просторового трикутника. Якщо, наприклад, точки 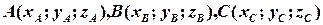є вершинами трикутника і цей трикутник добудувати до паралелограма

то, з одного боку, площа трикутника дорівнює половині площі паралелограма, а з іншого боку, площа паралелограма дорівнює довжині векторного добутку векторів, які лежать на сторонах паралелограма. Звідси маємо:

.

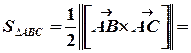
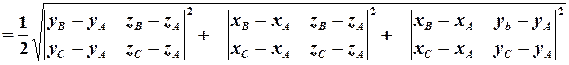Цікавим, з дуже красивою остаточною формулою, є випадок, коли обчислюється площа не просторового трикутника, а, наприклад, заданого координатами своїх вершин, що лежать на координатній площині:

.

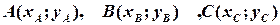Цей випадок пропонуємо розглянути самостійно.