 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
ВВЕДЕНИЕ 6 страница
|
|
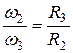 , откуда
, откуда 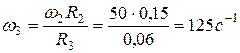 ,
,
что соответствует частоте вращения:
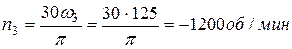 .
.
ПРЕОБРАЗОВАНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА В МЕХАНИЗМАХ.
Пример №8.
Механизм состоит из ступенчатых колес 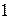 и
и  , связанных ременной передачей, колеса
, связанных ременной передачей, колеса  и
и 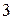 находятся в зацеплении, колесо
находятся в зацеплении, колесо 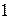 находится в зацеплении с зубчатой рейкой
находится в зацеплении с зубчатой рейкой 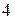 , груз
, груз 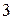 находится на конце нити, намотанной на шкив радиуса
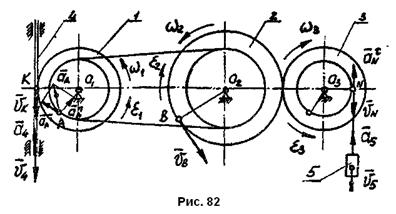
находится на конце нити, намотанной на шкив радиуса  (рис. 82). Определить скорости точек
(рис. 82). Определить скорости точек  и
и 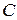 , ускорение груза
, ускорение груза 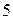 , ускорение точки
, ускорение точки  и угловое ускорение колеса
и угловое ускорение колеса  в момент времени
в момент времени 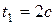 , если задан закон движения рейки
, если задан закон движения рейки 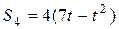 и размеры колес:
и размеры колес:
 ,
, 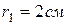 ,
, 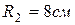 ,
, 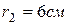 ,
,
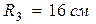 ,
, 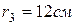 .
.
Решение:
1. Рейка 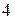 совершает поступательное движение по закону
совершает поступательное движение по закону 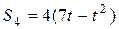 . Определим скорость движения рейки:
. Определим скорость движения рейки:
 . При
. При 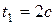 ,
, 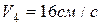 .
.
Ускорение рейки: 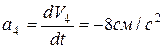 .
.
Знак минус указывает, что рейка движется замедленно.
2. Точка 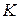 , лежащая на ободе колеса
, лежащая на ободе колеса 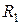 , движется со скоростью, равной скорости рейки, находящейся в зацеплении с колесом, т.е.
, движется со скоростью, равной скорости рейки, находящейся в зацеплении с колесом, т.е.
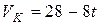 .
.
Учитывая, что 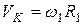 , можно выразить угловую скорость колеса
, можно выразить угловую скорость колеса 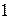 :
:
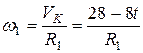 .
.
Угловое ускорение колеса 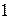 :
:
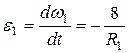 .
.
Колеса радиусов 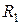 и
и 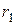 находятся на одном валу. Определим ускорение точки
находятся на одном валу. Определим ускорение точки  :
:
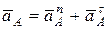 ,
,
где 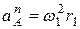 ,
,  ,
, 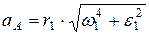
3. Колеса радиусов 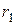 и
и 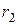 связаны бесконечным ремнем, поэтому скорости всех точек ремня одинаковы, т.е.
связаны бесконечным ремнем, поэтому скорости всех точек ремня одинаковы, т.е. 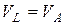 , угловые скорости и угловые ускорения валов
, угловые скорости и угловые ускорения валов 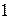 и
и  обратно пропорциональны
обратно пропорциональны
размерам колес:
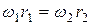 ;
; 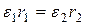 ;
;
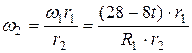 ;
; 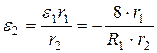 .
.
Скорость точки  , лежащей на ободе колеса
, лежащей на ободе колеса  :
:
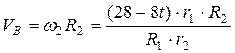 .
.
4. Колеса радиусов 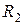 и
и 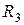 находятся в жестком зацеплении друг с другом, поэтому
находятся в жестком зацеплении друг с другом, поэтому
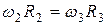 ;
; 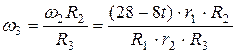 ;
;
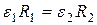 ;
;  .
.
Скорость точки 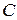 , лежащей на ободе колеса
, лежащей на ободе колеса 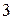 радиуса
радиуса  :
:
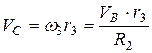 .
.
5. Ускорение груза 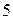 равно касательному ускорению точки
равно касательному ускорению точки 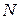 :
:
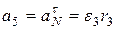 .
.
Для заданного момента времени 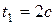 :
:
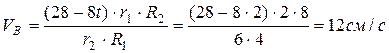 ;
;
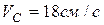 ;
;
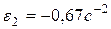 ;
;
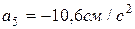 ;
;
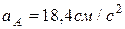 .
.
2.8. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА.
Плоскопараллельным (или просто плоским) называется такое движение твердого тела, при котором все его точки перемещаются в плоскостях, параллельных какой-то неподвижной плоскости. Плоское движение совершают многие звенья механизмов и машин, катящееся колесо.
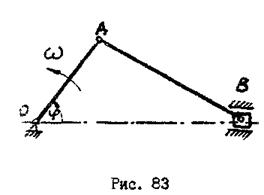 Частным случаем такого движения является вращение тела вокруг неподвижной оси. Все звенья кривошипно-ползунного механизма (рис.83), состоящего из кривошипа
Частным случаем такого движения является вращение тела вокруг неподвижной оси. Все звенья кривошипно-ползунного механизма (рис.83), состоящего из кривошипа  , ползуна
, ползуна  и шарнирно соединенного с ним шатуна
и шарнирно соединенного с ним шатуна  , совершают плоское движение, так как все звенья движутся параллельно некоторой неподвижной плоскости (плоскости чертежа). Одновременно движение кривошипа
, совершают плоское движение, так как все звенья движутся параллельно некоторой неподвижной плоскости (плоскости чертежа). Одновременно движение кривошипа  является вращательным, движение ползуна
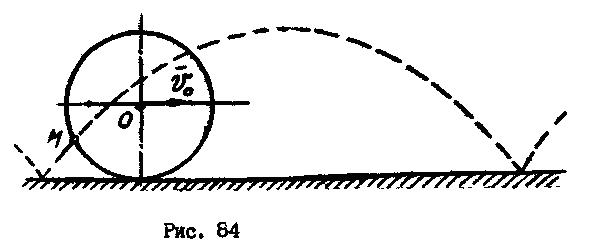
является вращательным, движение ползуна  - поступательным. Все точки колеса (рис. 84) движутся в плоскостях, параллельных неподвижной вертикальной плоскости. При движении по закруглению движение колеса не будет плоским.
- поступательным. Все точки колеса (рис. 84) движутся в плоскостях, параллельных неподвижной вертикальной плоскости. При движении по закруглению движение колеса не будет плоским.
Плоскопараллельное движение твердого тела является составным, оно складывается из поступательного движения вместе с какой-либо точкой, принятой за полюс, и вращения вокруг оси, проходящей через эту точку (рис.85). Поэтому плоское движение твердого тела описывается тремя уравнениями:
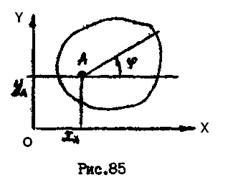
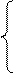

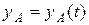 (2.31)
(2.31)
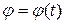
За полюс обычно принимают точку, скорость которой известна или ее легко можно вычислить. Например, движение колеса (рис.87) складывается из поступательного движения вместе с полюсом-центром колеса  и вращения с угловой скоростью
и вращения с угловой скоростью  вокруг оси, проходящей через полюс. Скорость любой точки
вокруг оси, проходящей через полюс. Скорость любой точки  тела, совершающего плоское движение, равна геометрической сумме скорости полоса и скорости точки в ее вращении вместе с телом вокруг оси, проходящей через полюс (рис.86):
тела, совершающего плоское движение, равна геометрической сумме скорости полоса и скорости точки в ее вращении вместе с телом вокруг оси, проходящей через полюс (рис.86):
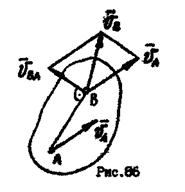
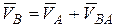 , (2.32)
, (2.32)
где 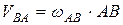 ,
,
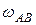 - угловая скорость звена.
- угловая скорость звена.
Вектор скорости 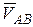 во вращательном движении направлен перпендикулярно к отрезку
во вращательном движении направлен перпендикулярно к отрезку  .
.
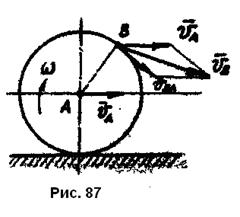 Скорость точки
Скорость точки  колеса (рис.87) складывается из скорости полюса-центра колеса
колеса (рис.87) складывается из скорости полюса-центра колеса  и скорости
и скорости 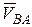 во вращении точки
во вращении точки  вместе с колесом относительно оси
вместе с колесом относительно оси  .
.
ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ТЕЛА
МЕТОДОМ ПОЛЮСА.
Пример №9.
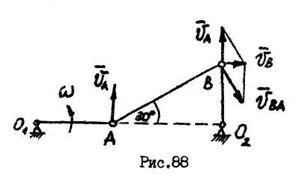
Для заданного положения шарнирного четырехзвенника (рис.88) определить скорость точки  и угловую скорость звена
и угловую скорость звена  , если кривошип
, если кривошип 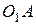 вращается с постоянной угловой скоростью
вращается с постоянной угловой скоростью 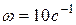 ,
, 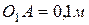 ,
, 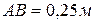 .
.
 Решение:
Решение:
1. Определим скорость точки  , принадлежащей кривошипу
, принадлежащей кривошипу 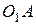 :
:
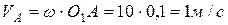 .
.
2. Определим скорость точки  , принимая за полюс точку
, принимая за полюс точку  :
:
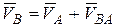 ,
, 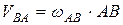 , (1)
, (1)
где 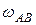 - угловая скорость звена
- угловая скорость звена  .
.
Спроецируем векторное равенство (1) на оси 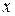 и
и 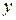 , направляя ось
, направляя ось 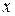 вдоль звена
вдоль звена  .
.
На ось 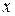 :
: 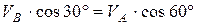 ;
;
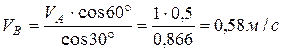 ;
;
На ось 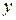 :
:  ;
;
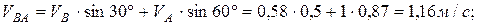
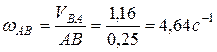 .
.
Проекции скоростей двух точек тела на прямую, соединяющую эти точки, равны между собой.
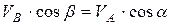 (2.33)
(2.33)
ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ТЕЛА ПО ТЕОРЕМЕ
О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА.
Пример №10.
Стержень 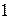 в точке
в точке  шарнирно связан со стержнем
шарнирно связан со стержнем  , который в точке
, который в точке  скользит по наклонной плоскости (рис.90). Определить скорость точки
скользит по наклонной плоскости (рис.90). Определить скорость точки  стержня
стержня  в положении, когда
в положении, когда 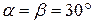 и скорость
и скорость 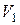 стержня
стержня 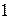 равна
равна 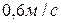 .
.
Решение:
1. Стержень 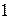 совершает поступательное движение, следовательно, скорость точки
совершает поступательное движение, следовательно, скорость точки  равна скорости
равна скорости 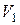 .
.
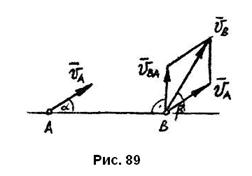
2. Скорость 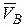 точки
точки  направлена вдоль плоскости, наклоненной к горизонту под углом
направлена вдоль плоскости, наклоненной к горизонту под углом 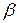 . Применим теорему о проекциях скоростей двух точек на прямую, соединяющую эти точки:
. Применим теорему о проекциях скоростей двух точек на прямую, соединяющую эти точки:
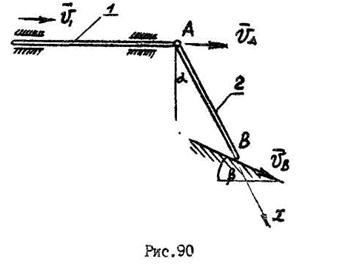
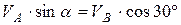 , откуда
, откуда

При определении скоростей точек тела за полюс можно принять точку  , скорость которой равна
, скорость которой равна 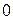 . Такую точку называют мгновенным центром скоростей (МЦС). В этом случае скорость любой точки тела будет равна:
. Такую точку называют мгновенным центром скоростей (МЦС). В этом случае скорость любой точки тела будет равна:
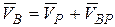 (2.34)
(2.34)
где 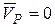 .
.
Следовательно, скорость любой точки тела пропорциональна расстоянию этой точки до МЦС (рис.91):
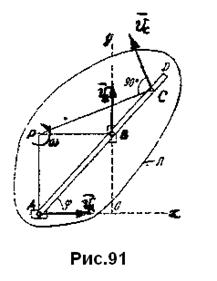
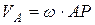 ;
;
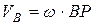 ,
,
т.е. для всех точек тела соблюдается соотношение:
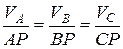 . (2.35)
. (2.35)
При определении положения мгновенного центра скоростей (МЦС) возможны следующие случаи:
1. Положение МЦС заранее известно (рис.92).
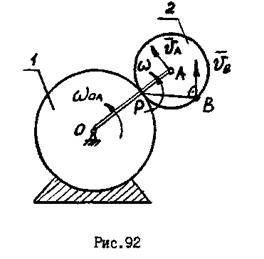 Если колесо
Если колесо  обкатывается по неподвижному колесу
обкатывается по неподвижному колесу  , то МЦС - точка
, то МЦС - точка  находится в точке касания этих колес.
находится в точке касания этих колес.
Скорость точки  , принадлежащей кривошипу
, принадлежащей кривошипу  :
:
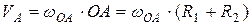 .
.
Угловая скорость колеса  :
:
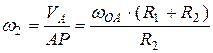 .
.
Скорость точки  пропорциональна расстоянию
пропорциональна расстоянию 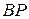 :
:
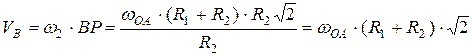 .
.
Вектор 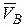 скорости точки
скорости точки  направлен перепендикулярно отрезку
направлен перепендикулярно отрезку 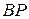 .
.
ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ТЕЛА С ПОМОЩЬЮ
МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ.
Пример №11.
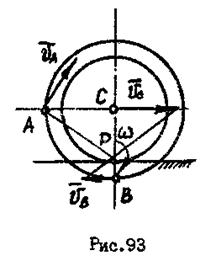
Определить скорости точек  и
и  ступенчатого колеса, имеющего размеры
ступенчатого колеса, имеющего размеры 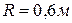 ,
, 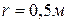 (рис.93), если скорость центра колеса
(рис.93), если скорость центра колеса 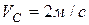 .
.
 Решение:
Решение:
Мгновенный центр ступенчатого колеса находится в точке  , где колесо касается неподвижной поверхности. Для скоростей точек колеса можно составить соотношение:
, где колесо касается неподвижной поверхности. Для скоростей точек колеса можно составить соотношение:
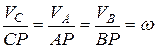
Угловая скорость колеса:
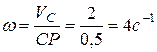 .
.
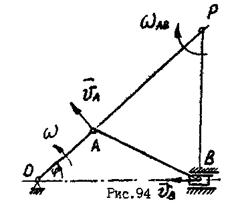
2. Если известны по направлению скорости двух точек тела и модуль скорости одной точки, то МЦС находится на пересечении перпендикуляров, проведенных к векторам скоростей этих точек. Если для кривошипно-ползунного механизма (рис.94) задана угловая скорость ведущего звена, то скорость точки  можно определить по формуле:
можно определить по формуле:
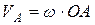 .
.
Вектор 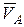 скорости точки
скорости точки  направлен перпендикулярно звену
направлен перпендикулярно звену  . Ползун
. Ползун  движется поступательно в горизонтальных направляющих, т.е. направление скорости точки
движется поступательно в горизонтальных направляющих, т.е. направление скорости точки  известно. МЦС звена
известно. МЦС звена  находится на пересечении перпендикуляров
находится на пересечении перпендикуляров  и
и 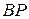 , проведенных к векторам скоростей
, проведенных к векторам скоростей 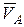 и
и 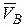 .
.
 Для определения скорости точки
Для определения скорости точки  и угловой скорости шатуна
и угловой скорости шатуна  можно составить соотношение:
можно составить соотношение:
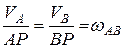 .
.
Пример №12.
Конец  стержня
стержня  скользит со скоростью
скользит со скоростью 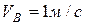 по наклонной плоскости. Другой конец
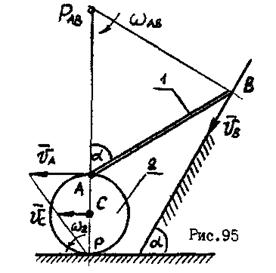
по наклонной плоскости. Другой конец  шарнирно связан с роликом, который катится без скольжения (рис.95). Определить скорость центра
шарнирно связан с роликом, который катится без скольжения (рис.95). Определить скорость центра 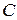 ролика и угловую скорость ролика, если угол
ролика и угловую скорость ролика, если угол 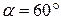 .
.
 Решение:
Решение:
Мгновенный центр скоростей ролика находится в точке  , где ролик касается неподвижной поверхности. Векторы
, где ролик касается неподвижной поверхности. Векторы 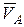 и
и 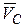 скоростей точек
скоростей точек  и
и 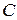 направлены перпендикулярно линии
направлены перпендикулярно линии  .
.
Скорость точки  определим с помощью мгновенного центра скоростей звена
определим с помощью мгновенного центра скоростей звена  , который находится в точке
, который находится в точке 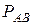 на пересечении перпендикуляров, проведенных к векторам скоростей
на пересечении перпендикуляров, проведенных к векторам скоростей 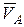 и
и 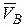 . Скорости
. Скорости 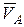 и
и 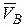 пропорциональны расстояниям соответствующих точек до МЦС:
пропорциональны расстояниям соответствующих точек до МЦС:
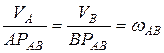 .
.
Так как 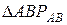 - равносторонний,
- равносторонний, 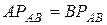 ,
,
 .
.
Скорости точек  и
и 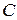 ролика с его угловой скоростью связаны соотношением:
ролика с его угловой скоростью связаны соотношением:
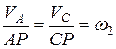 ,
,
где 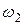 - угловая скорость ролика;
- угловая скорость ролика;
 ;
;
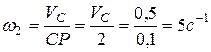 .
.
3. Если скорости точек  и
и  тела параллельны между собой, а линия
тела параллельны между собой, а линия  не перпендикулярна вектору
не перпендикулярна вектору 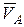 (рис.96), то мгновенный центр скоростей звена
(рис.96), то мгновенный центр скоростей звена  будет находиться в бесконечности. Так как
будет находиться в бесконечности. Так как 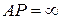 ,
,  , угловая скорость звена
, угловая скорость звена  будет равна нулю, что видно из соотношения:
будет равна нулю, что видно из соотношения:
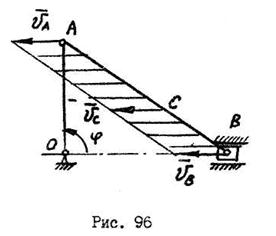
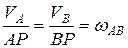 .
.
Шатун  при повороте ведущего звена на
при повороте ведущего звена на 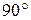 совершает мгновенно поступательно движение. Для такого движения скорости всех точек звена равны между собой:
совершает мгновенно поступательно движение. Для такого движения скорости всех точек звена равны между собой:
Дата публикования: 2014-10-20; Прочитано: 1586 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
