 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
ВВЕДЕНИЕ 3 страница. 2) изобразить заданные силы, действующие на систему тел
|
|
1) выделить составную конструкцию, равновесие которой рассматривается;
2) изобразить заданные силы, действующие на систему тел;
3) отбросить внешние связи, заменив их реакциями;
4) выбрать систему координат;
5} определить пути решения задачи: рассматривать равновесие каждой части конструкции в отдельности или равновесие системы в целом и одной из частей конструкции; прежде всего следует рассматривать те части составной конструкции, для которых из составленных уравнений равновесия можно определить искомые величины;
6) решить составленную систему уравнений равновесия относительно неизвестных величин;
7) проверить правильность решения, составляя неиспользованные в расчете уравнений равновесия для всей, конструкции.
Пример №7.
Определить нагрузку на каждую из пяти (А, В, С, D, E) осей автотягача с седельным полуприцепом (рис.43).
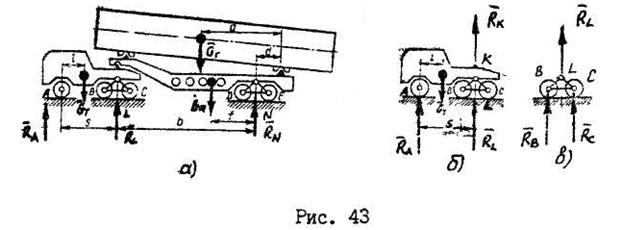
Решение:
Автотягач состоит из трех частей: шасси весом 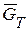 , полуприцепа весом
, полуприцепа весом 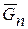 и кузова весом
и кузова весом 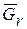 . Рассмотрим равновесие одной части конструкции – шасси (рис. 43,б). Действие отброшенной части заменим реакцией связи
. Рассмотрим равновесие одной части конструкции – шасси (рис. 43,б). Действие отброшенной части заменим реакцией связи 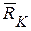 . Реакциями внешних связей для шасси являются
. Реакциями внешних связей для шасси являются 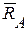 и
и 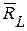 . Для нахождения реакции
. Для нахождения реакции 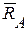 составим сумму моментов относительно точки
составим сумму моментов относительно точки  :
:
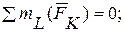
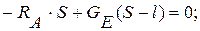 (1)
(1)
Откуда 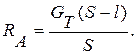 (2)
(2)
Рассматривая равновесие составной конструкции (рис. 43,а), найдем реакции остальных внешних связей 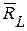 и
и 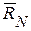 :
:
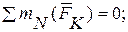
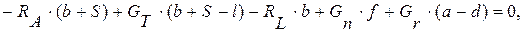 (2)
(2)
Откуда с учетом (2) выразим:
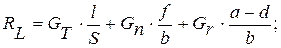 (3)
(3)
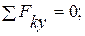
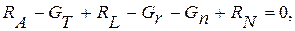 (4)
(4)
откуда с учетом (3) выразим:
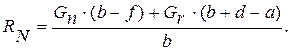 (4)
(4)
Учитывая симметричный характер нагрузки на оси (рис.43,в), определим реакции:
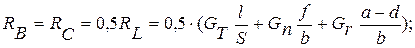
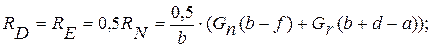
Пример №8.
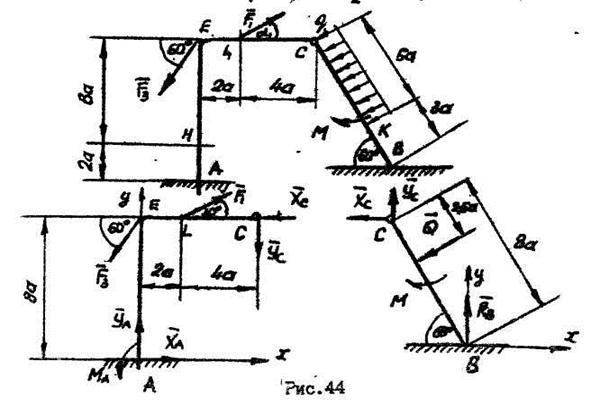
Определить реакции внешних и внутренних связей конструкции, состоящей из жесткого угольника и стержня (рис.44), соединенных шарнирно в точке С. На составную конструкцию действуют силы 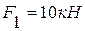 и
и 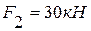 , равномерно распределенная нагрузка интенсивностью
, равномерно распределенная нагрузка интенсивностью 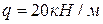 , пара сил с моментом
, пара сил с моментом 
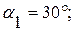
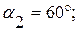
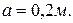
|
Решение:
Внешними связями, наложенными на конструкцию, является жесткая заделка в точке А и свободное опирание на гладкую поверхность в точке В. Внутренней связью является шарнирно С, с помощью которого соединены между собой части конструкции в отдельности, начиная расчет с равновесия стержня, у которого неизвестны три реакции связей 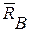 ,
, 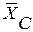 и
и 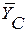 . Действие равномерно распределенной нагрузки интенсивностью
. Действие равномерно распределенной нагрузки интенсивностью 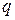 заменим сосредоточенной силой
заменим сосредоточенной силой  :
:
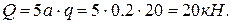
Выбираем систему координат и составляем три уравнения равновесия для стержня ВС:
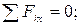
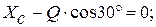 (1)
(1)
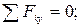
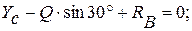 (2)
(2)
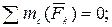
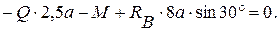 (3)
(3)
из (1): 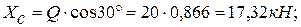
из (2): 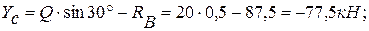
из (3): 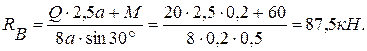
Действительное направление реакции 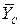 противоположно показанному на чертеже. Рассматриваем равновесие левой части конструкции. Составляющие реакции внутренней связи
противоположно показанному на чертеже. Рассматриваем равновесие левой части конструкции. Составляющие реакции внутренней связи 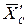 и
и 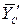 направлены в стороны, противоположные направлениям составляющих
направлены в стороны, противоположные направлениям составляющих 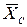 и
и 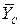 .
.
Составим три уравнения равновесия для левой части конструкции:
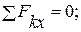
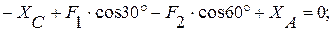 (4)
(4)
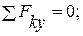
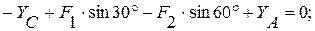 (5)
(5)
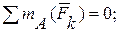
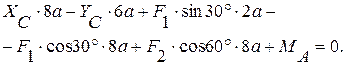 (6)
(6)
из (4): 
из (5): 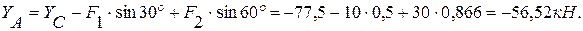
из (6): 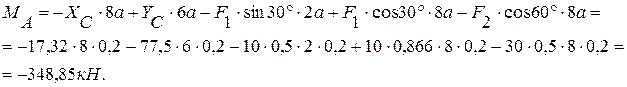
Для проверки составим уравнения равновесия для системы в целом:

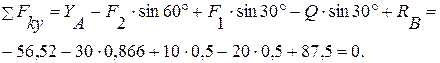
1.18.ПРОСТРАНСТВЕННАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ.
Условие равновесия пространственной системы сходящихся сил определяется тремя уравнениями:
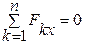 ;
; 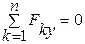 ;
;  . (18.1)
. (18.1)
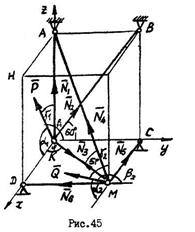
Пример №9. Определить усилия в шести стержнях, соединенных своими концами шарнирно друг с другом и с неподвижными опорами. В узлах К и М приложены силы 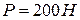 и
и 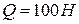 , составляющие с положительным направлением координатных осей углы, равные соответственно
, составляющие с положительным направлением координатных осей углы, равные соответственно 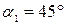 ,
,  ,
, 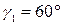 для силы
для силы 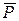 и
и 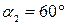 ,
, 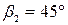 ,
, 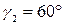 для силы
для силы 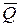 . Взаимное расположение стержней в конструкции определяется углами
. Взаимное расположение стержней в конструкции определяется углами 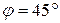 и
и 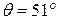 (рис.45).
(рис.45).
 Решение:
Решение:
Так как для системы сходящихся сил можно составить три уравнения равновесия, расчет начинаем с узла К, в котором сходятся стержни 1,2,3. Предполагаем все стержни растянутыми. Растягивающие усилия в стержнях 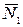 ,
, 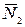 и
и 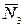 направлены от узла К. Составим три уравнения равновесия:
направлены от узла К. Составим три уравнения равновесия:
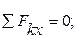
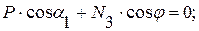 (1)
(1)
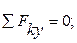
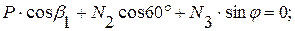 (2)
(2)
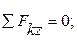
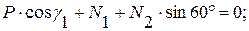 (3)
(3)
из (1): 
из (2): 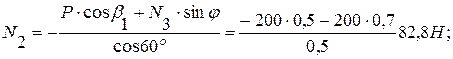
из (3): 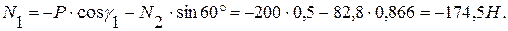
Рассмотрим равновесие узла  . Усилия
. Усилия 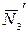 и
и 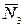 равны по модулю и противоположны по направлению. Усилие
равны по модулю и противоположны по направлению. Усилие 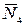 составляет с плоскостью
составляет с плоскостью 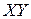 угол
угол 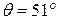 . Для нахождения проекции усилия
. Для нахождения проекции усилия 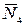 на координатные оси, необходимо предварительно найти проекцию на плоскость
на координатные оси, необходимо предварительно найти проекцию на плоскость 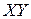 , а затем составляющие этой проекции на каждой из координатных осей. Составим три уравнения равновесия для системы сходящихся сил, приложенных к узлу
, а затем составляющие этой проекции на каждой из координатных осей. Составим три уравнения равновесия для системы сходящихся сил, приложенных к узлу  :
:
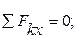
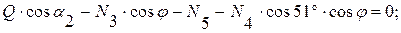 (4)
(4)
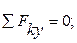
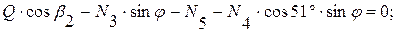 (5)
(5)
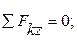
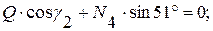 (6)
(6)
из (6): 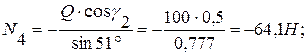
из (4): 
из (5): 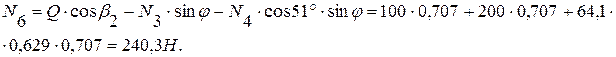
Знаки показывают, что стержни 1,3,4 – сжаты, а 2,5,6 – растянуты.
1.19. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ.
Для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно соблюдения следующих условий:
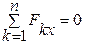 ;
; 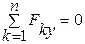 ;
; 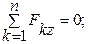
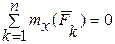 ;
; 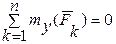 ;
; 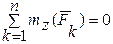 . (19.1)
. (19.1)
Следовательно, число неизвестных не должно превышать числа возможных уравнений равновесия. В некоторых случаях число возможных уравнений равновесия может быть уменьшено. Так, если все силы, приложенные к твердому телу, лежат в плоскости  , то уравнения проекций этих сил на ось
, то уравнения проекций этих сил на ось  обращаются в тождество, и число уравнений равновесия сокращается до пяти.
обращаются в тождество, и число уравнений равновесия сокращается до пяти.
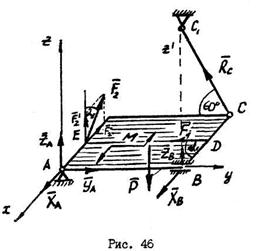
Пример №10.
Однородная прямоугольная плита весом 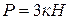 со сторонами
со сторонами 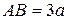 и
и 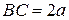 закреплена в точке
закреплена в точке  сферическим шарниром, в точке
сферическим шарниром, в точке  цилиндрическим шарниром и удерживается в равновесии невесомым стержнем
цилиндрическим шарниром и удерживается в равновесии невесомым стержнем 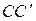 (рис.46). На плиту действует пара сил с моментом
(рис.46). На плиту действует пара сил с моментом 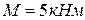 и силы
и силы 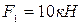 и
и 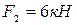 . Сила
. Сила 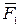 лежит в плоскости
лежит в плоскости 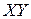 и составляет с осью
и составляет с осью 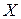 угол
угол  , сила
, сила 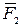 лежит в плоскости
лежит в плоскости 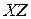 и составляет с осью
и составляет с осью 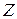 угол
угол 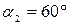 .
.
Определить реакции связей при 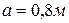 ,
,  ,
, 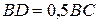 .
.
 Решение:
Решение:
На плиту действуют активные силы 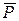 ,
, 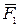 ,
, 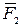 , пара сил с моментом
, пара сил с моментом 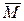 , а также реакции связей. Реакцию сферического шарнира
, а также реакции связей. Реакцию сферического шарнира  разложим на три составляющие
разложим на три составляющие 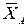 ,
, 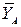 ,
, 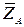 , цилиндрического шарнира
, цилиндрического шарнира  (подшипника) – на две составляющие
(подшипника) – на две составляющие  и
и 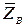 , реакцию
, реакцию 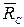 невесомого стержня направим вдоль стержня, предполагая, что он растянут. Для определения шести неизвестных реакций связей составим шесть уравнений равновесия действующих на плиту сил:
невесомого стержня направим вдоль стержня, предполагая, что он растянут. Для определения шести неизвестных реакций связей составим шесть уравнений равновесия действующих на плиту сил:
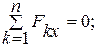
 (1)
(1)
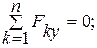
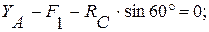 (2)
(2)
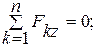
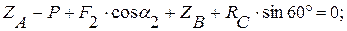 (3)
(3)
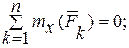
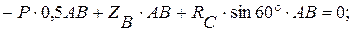 (4)
(4)
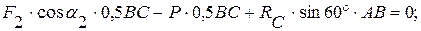 (5)
(5) 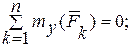
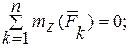
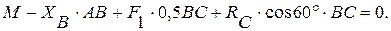 (6)
(6)
Для определения момента силы 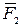 относительно координатных осей, раскладываем силу
относительно координатных осей, раскладываем силу 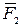 на две составляющие
на две составляющие 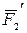 и
и  , численно равные проекциям этой силы на оси Z и X соответственно:
, численно равные проекциям этой силы на оси Z и X соответственно: 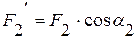 ,
, 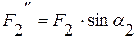 .
.
Решая систему уравнений (1)-(6), находим искомые величины:
из (5): 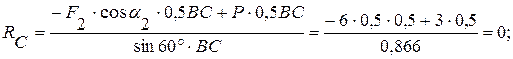
из (6): 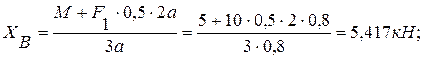
из (1): 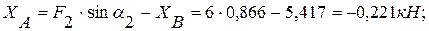
из (2): 
из (4): 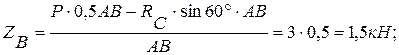
из (3): 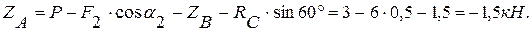
Для проверки можно составить уравнение моментов относительно оси  , проведенной через точку
, проведенной через точку  :
:
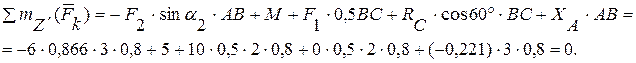
Реакции связей, значения которых получены отрицательными, имеют направления, противоположное показанному на чертеже.
Пример №11.
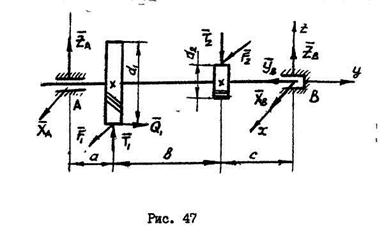
На косозубое колесо вала редуктора диаметром 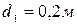 действует осевая сила
действует осевая сила 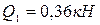 , радиальная
, радиальная 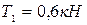 и неизвестное окружное усилие
и неизвестное окружное усилие 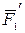 . На прямозубое колесо диаметром
. На прямозубое колесо диаметром 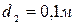 , закрепленное на том же валу, действует радиальная сила
, закрепленное на том же валу, действует радиальная сила 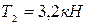 (рис. 47).
(рис. 47).
Определить реакции подшипников при следующих размерах:  ;
; 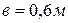 ;
; 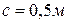 .
.
|
Решение:
Опорой горизонтального вала в точке  является радиальный подшипник, его реакцию раскладываем на две составляющие
является радиальный подшипник, его реакцию раскладываем на две составляющие 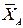 и
и 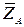 . В точке
. В точке  - радиально-упорный подшипник. Его реакцию раскладываем на три составляющие
- радиально-упорный подшипник. Его реакцию раскладываем на три составляющие  ,
, 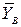 ,
, 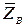 . Шестой неизвестной величиной является окружное усилие
. Шестой неизвестной величиной является окружное усилие 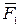 . Составим для вала шесть уравнений равновесия:
. Составим для вала шесть уравнений равновесия:
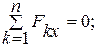
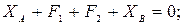 (1)
(1)
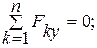
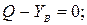 (2)
(2)
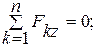
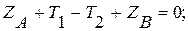 (3)
(3)
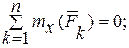
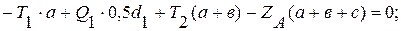 (4)
(4)
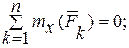
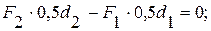 (5)
(5)
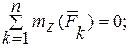
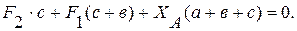 (6)
(6)
Решая систему уравнений (1)-(6), находим неизвестные величины:
из (2): 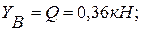
из (5): 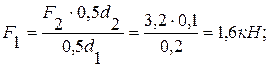
из (6): 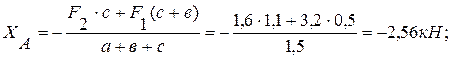
из (1): 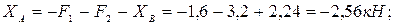
из (4): 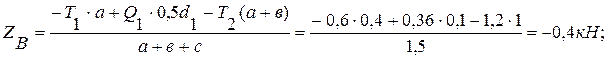
из (3): 
1.20. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА.
Центром тяжести твердого тела называется точка, через которую проходит линия действия равнодействующей сил тяжести частиц данного тела при любом положении тела в пространстве. Силы тяжести отдельных частиц тела образуют систему параллельных сил. Координаты центра тяжести как центра параллельных сил можно определить по формулам:
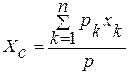 ;
; 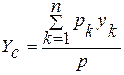 ;
; 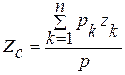 ; (20.1)
; (20.1)
где 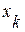 ,
, 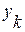 ,
, 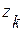 - координаты точек приложенных сил тяжести частиц тела.
- координаты точек приложенных сил тяжести частиц тела.
Положение центра тяжести однородного тела зависит только от геометрической формы тела. Координаты центра тяжести пластины определятся формулами:
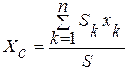 ;
; 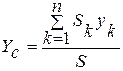 , (20.2)
, (20.2)
где  - площадь всей пластины;
- площадь всей пластины;
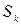 - площадь части пластины.
- площадь части пластины.
Аналогично можно выразить координаты центра тяжести линии:
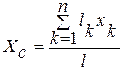 ;
; 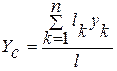 ;
; 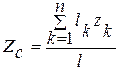 , (20.3)
, (20.3)
где 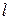 - длина всей линии;
- длина всей линии;
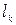 - длина участка линии.
- длина участка линии.
При определении координат центра тяжести тела плоской формы, тело разбивают на конечное число частей, для каждой из которых положение центра тяжести известно и используют формулы (20.2) или (20.3). Например, координаты центра тяжести пластины, изображенной на рис.48, можно определить двумя способами:
1. Разбить пластину на прямоугольники 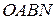
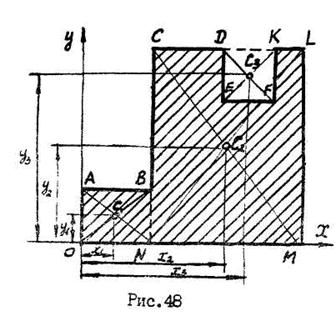 ,
, 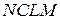 и вырез
и вырез 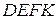 . Тогда
. Тогда
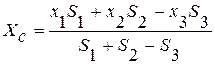 ;
;
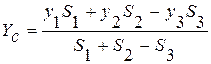 ;
;
где 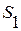 ,
,  ,
, 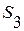 - площади частей пластины и выреза.
- площади частей пластины и выреза.
Дата публикования: 2014-10-20; Прочитано: 323 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
