 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Поток вектора напряженности
|
|
Электрическое поле можно задать, указав для каждой точки величину и направление вектора  . Совокупность этих векторов образует поле вектора напряженности электрического поля. Электрическое поле можно описать с помощью линий напряженности (линий
. Совокупность этих векторов образует поле вектора напряженности электрического поля. Электрическое поле можно описать с помощью линий напряженности (линий  ), которые проводятся так, чтобы касательная к ним в каждой точке совпадала с направлением вектора
), которые проводятся так, чтобы касательная к ним в каждой точке совпадала с направлением вектора  . Густота линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности перпендикулярной к линиям площадки, было равно численному значению вектора
. Густота линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности перпендикулярной к линиям площадки, было равно численному значению вектора  . Линии
. Линии  точечного заряда представляют собой совокупность радиальных прямых, направленных от заряда, если он положителен, и к заряду, если он отрицателен. Линии одним концом опираются на заряд, другим уходят в бесконечность. Покажем это. Полное число линий N, пересекающих сферическую поверхность произвольного радиуса r, будет равно произведению густоты линий на поверхность сферы 4 pr 2. Густота линий по условию численно равна
точечного заряда представляют собой совокупность радиальных прямых, направленных от заряда, если он положителен, и к заряду, если он отрицателен. Линии одним концом опираются на заряд, другим уходят в бесконечность. Покажем это. Полное число линий N, пересекающих сферическую поверхность произвольного радиуса r, будет равно произведению густоты линий на поверхность сферы 4 pr 2. Густота линий по условию численно равна
 .
.
Следовательно, N численно равна
 ,
,
т.е. полное число линий на любом расстоянии от заряда будет одно и то же. Следовательно, линии нигде, кроме заряда, не начинаются и не заканчиваются; они, начавшись на заряде, уходят в бесконечность, либо, приходя из бесконечности, заканчиваются на заряде.

Рис. 13.2.
Поскольку густота линий  выбирается равной численному значению Е, количество линий, пронизывающих площадку dS, перпендикулярных
выбирается равной численному значению Е, количество линий, пронизывающих площадку dS, перпендикулярных  будет численно равна ЕdS. Если площадка dS ориентирована так, что нормаль к ней образует с вектором
будет численно равна ЕdS. Если площадка dS ориентирована так, что нормаль к ней образует с вектором  угол a, то количество линий, пронизывающих площадку, будет численно равно ЕdS cos a= En dS, где En – составляющая вектора
угол a, то количество линий, пронизывающих площадку, будет численно равно ЕdS cos a= En dS, где En – составляющая вектора  по направлению нормали к площадке.
по направлению нормали к площадке.
Отсюда для количества линий  , пронизывающих произвольную поверхность, получается следующее выражение:
, пронизывающих произвольную поверхность, получается следующее выражение:
 .
.
Если имеется поле некоторого вектора 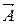 , то выражение
, то выражение  , где Ап – составляющая вектора
, где Ап – составляющая вектора 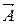 по направлению нормали к dS, называется потоком вектора
по направлению нормали к dS, называется потоком вектора 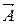 через поверхность S.
через поверхность S.
Следовательно, поток вектора 
 (13.7)
(13.7)
численно равен количеству линий  , пронизывающих поверхность S.
, пронизывающих поверхность S.
Дата публикования: 2014-10-04; Прочитано: 1093 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
