Поле бесконечно заряженного цилиндра

Рассмотрим поле, создаваемое бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной поверхностной плотностью s. Из соображений симметрии следует, что напряженность поля в любой точке должна быть направлена вдоль радиальной прямой, перпендикулярна к оси цилиндра, а величина напряженности может зависеть лишь от расстояние r от оси цилиндра.

Рис. 13.6.

Представим себе мысленно коаксиальную с заряженной поверхностью замкнутую цилиндрическую поверхность радиуса r и высотой h. Для оснований этого цилиндра Е_п = 0, для боковой поверхности Е_п = Е (r). Следовательно, поток линий 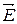через эту замкнутую поверхность будет равен Е (r)×2p× r × h. Если r > R, внутри поверхности попадает заряд 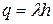, где l - линейная плотность заряда. Применяя теорему Гаусса, получаем

Е (r)×2p× r × h = ,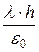

откуда Е (r)×= 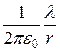. (13.13)

Если r < R, рассматриваемая замкнутая поверхность не содержит внутри зарядов, вследствие чего Е (r) = 0. Таким образом, внутри заряженной цилиндрической поверхности бесконечной длины поле отсутствует.