Закон Кулона. В этом выражении под следует подразумевать вектор, проведенный от одного заряда к другому и имеющий направление к тому из зарядов

В 1785 г. Кулон экспериментально, с помощью крутильных весов установил, что сила взаимодействия двух точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними

, (13.1)

где = 9×10⁹ Нм²/Кл²,

или в векторном виде

. (13.2)

В этом выражении под следует подразумевать вектор, проведенный от одного заряда к другому и имеющий направление к тому из зарядов, к которому приложена сила .

Рис. 13.1

В системе СИ . Тогда закон Кулона примет вид

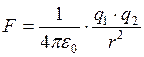. (13.3)

Здесь e ₀ = 8,85×10^-12 Кл²/Нм² – абсолютная диэлектрическая проницаемость вакуума.

Взаимодействие между зарядами осуществляется через электрическое поле. Всякий заряд изменяет свойства окружающего его пространства – создает в нем электрическое поле. Поле проявляет себя в том, что на помещенный в какую-либо его точку электрический заряд действует сила. По величине силы можно судить об «интенсивности» поля.

Силу, действующую на единичный положительный заряд, помещенный в данную точку поля, называют напряженностью электрического поля в этой точке

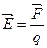. (13.4)

Из закона Кулона следует, что

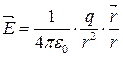. (13.5)

За единицу напряженности электрического поля принимается напряженность в такой же точке, в которой на заряд, равный единице действует единичная сила (в СИ 1к – заряд, 1н – сила). .

Опыт показывает, что сила, с которой система зарядов действует на некоторый не входящий в систему заряд, равна векторной сумме сил, с которыми действует на данный заряд каждый из зарядов системы в отдельности. Отсюда вытекает, что напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности:

(13.6)

это утверждение носит название принципа суперпозиции (наложения) электрических полей.