Классическое определение вероятности. Под опытом или экспериментом будем понимать всякое осуществление комплекса определенных условий, в результате которых будет происходить интересующее нас

Под опытом или экспериментом будем понимать всякое осуществление комплекса определенных условий, в результате которых будет происходить интересующее нас явление.

Будем считать фиксированным комплекс условий σ, который мы называем опытом, и будем рассматривать некоторую систему событий A, B, C,…, каждое из которых может либо произойти, либо не произойти.

Пример 1. Опыт σ: стрельба по мишени. Событие А – попадание по мишени. Событие В – промах.

Пример 2. Опыт σ: выбор изделий из партии готовых. Событие А – изделие браковано. Событие В – изделие стандартное.

Элементарным событием (или элементарным исходом) называется любой простейший, то есть неделимый в рамках данного эксперимента, исход опыта. Множество всех элементарных исходов будем называть пространством элементарных событий и обозначать Ω. То есть множество исходов опытов образует пространство элементарных событий, если:

в результате опыта один из исходов обязательно происходит;

появление одного из исходов опыта исключает появление остальных;

в рамках данного опыта нельзя разделить элементарный исход на более мелкие составляющие.

Записывают это так:

Ω ={w_1, w_2, …w_n,…}={w_k, k=1…n, …}.

Пример 3. Опыт: подбрасывание монеты 1 раз.

Здесь Ω={w_г, w_ц}, где w_г – выпадение герба, w_ц – выпадение цифры.

Опыт: монета подбрасывается 2 раза. В данном случае пространство элементарных событий Ω={w_{г г,}w_{г ц,} w_{ц г,}w_{ц ц} }.

Опыт заключается в определении числа вызовов, поступивших на телефонную станцию за время Т. Здесь Ω={0,1,2.…n,… }.

Любой набор элементарных исходов или произвольное подмножество А 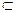Ω называется случайным событием.

Пусть Ω - пространство элементарных событий, S - некоторое подмножество случайных событий, удовлетворяющее следующим условиям:

Множество S – замкнуто относительно операций сложения, умножения и отрицания.

.

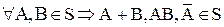Достоверное E и невозможное 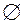события принадлежат S.

Иногда требуют большего: для любой бесконечной последовательности событий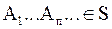

, .

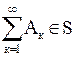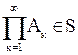Подмножество S, удовлетворяющее этим условиям, называется σ – алгеброй .

Пусть задана функция, которая каждому случайному событию из S ставит в соответствие число из интервала [0,1]; Р: S → [0,1], и при этом выполняются следующие аксиомы:

,

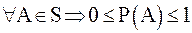Р(Е)=1, Р(Ø)=0,

Для любой последовательности А₁,…А_n… попарно несовместных событий А_iÎS,

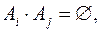"i, j, і≠ј,

.

Функцию Р, удовлетворяющую этим аксиомам, называют вероятностью, а значение Р(A) называют вероятностью события А.