Расчет продольных деформаций надземного участка трубопровода

Рассмотрим участок трубопровода между двумя анкерными опорами, включающий Z-образный компенсатор (рис. 51, а).

Рис. 51. Расчетная схема надземного трубопровода с Z-образным компенсатором

между двумя анкерными опорами

Расчетная схема представляет собой два прямолинейных участка, сопряженных компенсатором, который необходим для уменьшения внутренних сил и напряжений от продольных перемещений, возникающих от температурных перепадов и от внутреннего давления.

Чтобы решить эту задачу, достаточно определить распор компенсатора (рис. 51, б), который возникает от его сжатия при продольных перемещениях прямолинейных участков трубопровода.

Деформация компенсатора определяется сближением или удалением друг от друга его крайних сечений (мест соединения с прямолинейными трубами)

, (8.1)

где – продольные перемещения концевых сечений прямолинейных участков трубопровода.

Величина перемещений зависит от продольных сил , которые возникают от действия внутреннего давления в продольном направлении трубы, температурных деформаций трубы, поперечных деформаций трубы от внутреннего давления и от реакции компенсатора (распора компенсатора)

,

, (8.2)

где 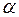– температурный коэффициент линейного расширения;

– температурный перепад; 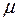– коэффициент Пуассона;

– длина прямолинейного участка трубопровода;

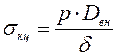– кольцевые напряжения трубы;

– продольная сила; – внутреннее давление.

Распор компенсатора пропорционален продольному перемещению

, (8.3)

где – жесткость компенсатора; – податливость компенсатора.

Продольное перемещение компенсатора

. (8.4)

Податливость Z-образного компенсатора была определена в первой части учебного пособия по формуле (10.17)

, (8.5)

где 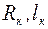– размеры компенсатора.

Таким образом, после подстановки в уравнение (8.1) всех перемещений получается уравнение с одним неизвестным . После решения этого уравнения можно вычислить все перемещения и напряжения участка трубопровода.