Устойчивость магистральных трубопроводов

УСТОЙЧИВОСТЬ МАГИСТРАЛЬНЫХ ТРУБОПРОВОДОВ

Одним из наиболее опасных явлений, которое может возникнуть при эксплуатации трубопровода, является потеря его продольной устойчивости. Это происходит, когда при действии положительного температурного перепада и внутреннего давления в поперечных сечениях трубопровода возникают сжимающие усилия. Ещё более опасным является вариант нагружения продольной сжимающей силой изогнутого трубопровода. Потеря устойчивости может привести к выпучиванию подземного трубопровода из траншеи, сопровождающемуся резким нарастанием прогибов и смятием трубы.

1.1. Потеря устойчивости прямого стержня под действием осевой сжимающей силы

Равновесие прямого стержня, сжимаемого осевыми силами, может быть устойчивым и неустойчивым.

При устойчивом равновесии прямолинейный сжимаемый стержень, выведенный из состояния равновесия, например, поперечной силой возвращает свою первоначальную форму после снятия внешней нагрузки.

При неустойчивом равновесии сжимаемый стержень, выведенный из состояния равновесия, продолжает деформироваться в направлении отклонения, а после прекращения воздействий в исходное состояние не возвращается.

Между двумя этими состояниями существует, так называемое, критическое состояние, характеризуемое критической сжимающей силой.

Достижение нагрузками критических значений равносильно разрушению конструкции, так как неустойчивая форма равновесия обязательно будет утрачена, а деформации и напряжения будут неограниченно расти.

При потере устойчивости (устойчивой формы равновесия) разрушение происходит внезапно от изгиба, когда прочность элемента на сжатие еще далеко не исчерпана.

Рассмотрим два способа определения критической силы. Первый из них классический метод Эйлера.

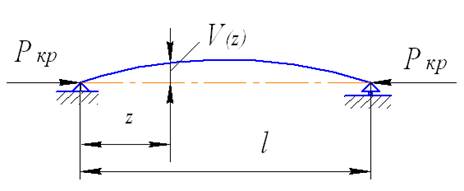
Рис. 1. Схема потери устойчивости прямого сжимаемого стержня

При потере устойчивости прямой стержень изгибается, а в поперечных сечениях возникает внутренний момент

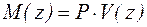. (1.1)

По теории стержней этот момент и прогибы связаны дифференциальной зависимостью

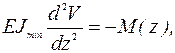
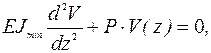
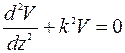, (1.2)

где .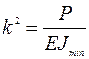

Решение дифференциального уравнения (2) имеет следующий вид

(1.3)

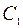где и 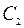– постоянные, определяемые из граничных условий.

При ,

. (1.4)

Отсюда .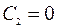

При ,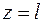

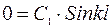. (1.5)

Поскольку 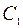не может равняться нулю получаем условие для определения критической сжимающей силы

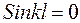. (1.6)

Решение этого тригонометрического уравнения

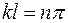. (1.7)

Подставляя в (7) выражение для 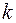и полагая, что для определения минимальной критической силы 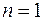, получим выражение для критической силы, которое называется формулой Эйлера

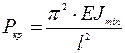. (1.8)

В основу второго метода расчета на устойчивость положен энергетический подход, и он позволяет рассматривать более сложные задачи. Для знакомства с этим методом рассмотрим предыдущую задачу

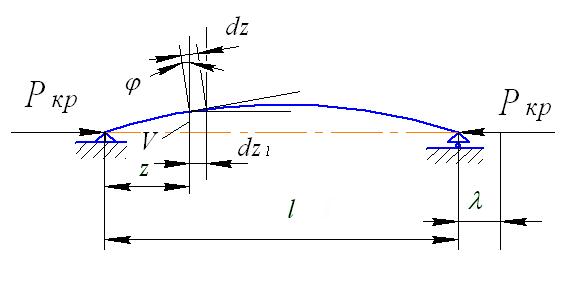
Рис. 2. Расчетная схема определения критической силы энергетическим методом

Согласно энергетическому принципу при потере устойчивости прямого стержня работа , совершенная силой , превращается в потенциальную энергию изогнутого стержня .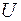

Потенциальную энергию деформации изогнутого стержня можно определить, если известно выражение для изгибающего момента

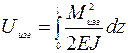. (1.9)

С учетом дифференциальной зависимости изгибающего момента и прогиба

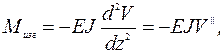
. (1.10)

Для вычисления работы необходимо выразить продольное перемещение , через поперечные перемещения 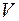. Для малых перемещений получаем

, (1.11)

где 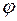– угол поворота поперечного сечения стержня.

Между прогибом 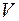и углом поворота 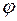, также существует дифференциальная зависимость

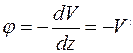. (1.12)

С учетом этого

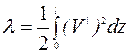. (1.13)

Работа силы

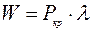. (1.14)

Приравнивая 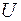и , получаем выражения для определения критической силы

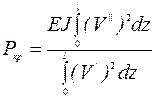. (1.15)

Таким образом, энергетический метод позволяет определить критическую силу , если задано уравнение прогибов . Важно отметить, что это уравнение может быть задано приближенно, но так чтобы оно удовлетворяло граничным условиям.

Для рассматриваемого примера (рис. 2) можно выразить прогиб тригонометрической функцией

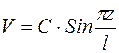. (1.16)

Получив первую и вторую производные от (1.16) и подставив в (1.15) легко получить точно формулу Эйлера (1.8). Это позволяет сделать вывод о том, что для решения практических задач можно применять приближенный энергетический метод и получать достаточно точные решения.

1.2. Поперечные перемещения подземного участка магистрального трубопровода

Продольные сжимающие усилия в трубопроводе, которые могут привести к потере его устойчивости, возникают от положительного температурного перепада и от внутреннего давления. При этом наиболее вероятным вариантом аварийных перемещений является выпучивание трубопровода из траншеи вверх. В связи с этим самыми опасными участками будут те, где магистральный трубопровод изогнут вверх.

С точки зрения механики стержней на расчетной схеме подземный трубопровод представляет собой прямой или изогнутый стержень, воспринимающий продольно поперечный изгиб (рис. 3).

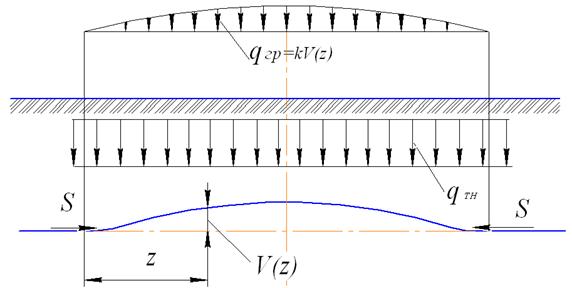
Рис. 3. Схема нагружения подземного трубопровода

Поперечные перемещения такого трубопровода будут зависеть от продольной силы 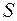, возникающей от воздействия положительных температурных перепадов и действия внутреннего давления, а также от поперечных нагрузок, вызванных собственным весом трубопровода с продуктом 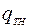и сопротивлением грунта .

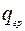Математическая модель для этого случая нагружения трубопровода будет иметь следующий вид

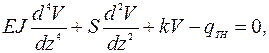(1.17)

где 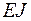– изгибная жесткость трубы;

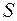– эквивалентное сжимающее усилие;

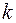– коэффициент сопротивления грунта поперечным перемещениям трубы;

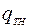– поперечная нагрузка от веса трубы и продукта.

Сжимающее усилие 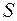может быть определено по методике [1], учитывающей сопротивление грунта продольным перемещениям и податливость деформируемого участка трубопровода.

Сопротивление грунта поперечным перемещениям трубопровода должно определяться в зависимости от направления изгиба трубы. Далее рассматривается методика оценки маханических характеристик грунта для случая, когда труба перемещается вертикально вверх из траншеи [2].

1.3. Сопротивление грунта поперечным перемещениям трубы

Механические характеристики грунта, с которым взаимодействует трубопровод, определяются экспериментально. Для решения поставленной выше задачи проводили испытания на трубах разного диаметра 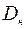одинаковой длины .

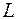Трубы укладывались на различную глубину 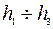(рис. 4) и затем поднимались лебедками с помощью тросов. Для каждого испытания строились диаграммы 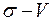. Вертикальное перемещение трубы вверх 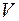измерялось специальными приборами. Нормальное давление на грунт определялось как отношение вертикальной силы 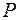к площади контакта грунта с трубой

. (1.18)

В процессе исследований были проанализированы результаты испытаний различных грунтов и установлено, что общий вид построенных диаграмм 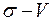аналогичен (рис. 4).

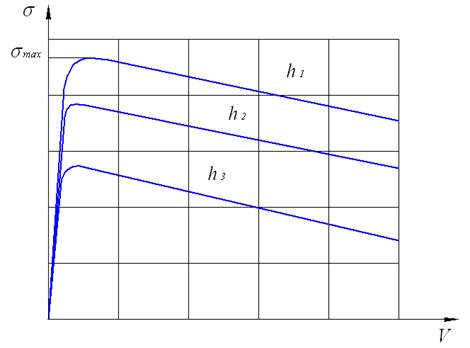
Рис. 4. Диаграмма сопротивления грунта

На первом участке диаграммы, когда перемещения 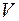малы, сопротивление грунта почти линейно пропорциональны этим перемещениям. Поэтому можно

полагать

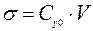, (1.19)

где 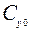– обобщенный коэффициент нормального сопротивления грунта.

Коэффициент 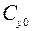зависит от свойств грунта и геометрических параметров заглубленного трубопровода.

После достижения максимума 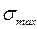сопротивление грунта начинает снижаться. Можно выделить второй участок, на котором происходит разгрузка трубы, также почти с линейной зависимостью между её перемещением и сопротивлением грунта.

При составлении расчетных математических моделей полученные экспериментальные результаты обычно представляют в виде зависимостей между погонной нагрузкой и поперечными перемещениями трубы 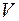. Реальная диаграмма испытаний (рис. 4) при этом заменяется билинейной (рис. 5). На такой идеализированной диаграмме выделяется характерная точка с перемещением 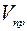, сопротивление грунта в которой считаются предельными 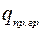. На участке, где перемещения меньше 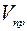, сопротивление грунта пропорционально перемещениям

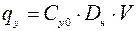. (1.20)

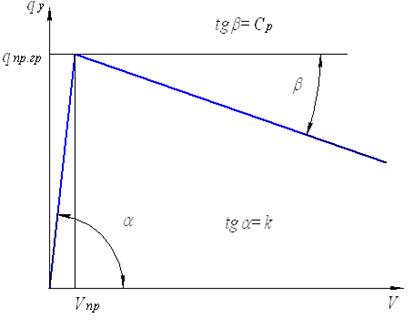
Рис. 5. Билинейная диаграмма сопротивления грунта поперечным перемещениям

На участке разгрузки, когда поперечные перемещения становятся больше 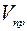, с некоторым приближением можно считать, что сопротивление грунта также, как на первом участке, пропорционально перемещениям и вычисляется по формуле

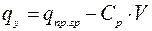, (1.21)

где 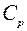– коэффициент разгрузки.

Предельная удерживающая способность грунта определяется призмой выпора. Для реальных трубопроводов можно считать, что угол откоса призмы определяется углом внутреннего трения грунта. Для определения предельного сопротивления грунта 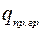можно использовать эмпирическую формулу, полученную на основании анализа экспериментальных данных, рекомендованную в работе [2]

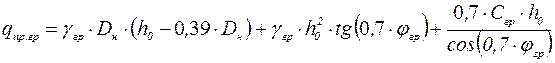, (1.22)

где 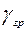– объемный вес грунта, Н/м²;

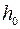– расстояние от верха засыпки до оси трубы, м;

– угол внутреннего трения грунта;

– сцепление грунта, Па.

Если считать, что при поперечных перемещениях трубы по величине равных глубине её заложения, сопротивление грунта равно нулю из формулы (1.21) получаем

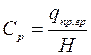, (1.23)

где – расстояние от верха засыпки до низа трубы.

1.4. Энергетический метод определения критической силы

Для анализа продольной устойчивости трубопровода с начальным изгибом (рис. 6) принимается модель грунта с ограниченным сопротивлением поперечным перемещениям вверх (рис. 5).

Для первого участка сопротивления грунта, 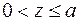(рис. 6), дифференциальное уравнение продольно-поперечного изгиба стержня (трубопровода) с начальным изгибом на упругом основании имеет следующий вид

(1.24)

где 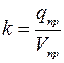– коэффициент пропорциональности, который в данном случае кроме сопротивления самого грунта учитывает вес трубопровода с продуктом

; (1.25)

и 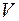– начальный и дополнительный прогибы сечений изогнутой трубы;

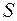– продольное сжимающее усилие в начале рассматриваемого участка изогнутого трубопровода.

Для второго участка,

. (1.26)

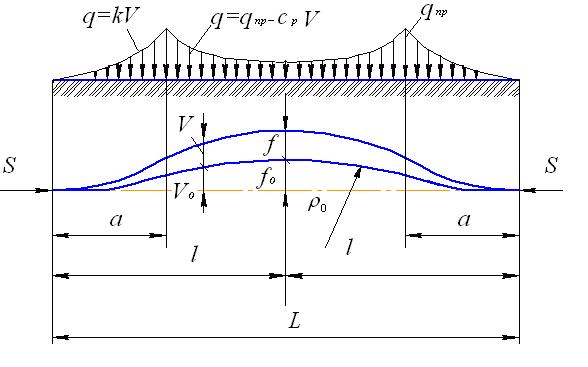
Рис. 6. Расчетная схема подземного трубопровода с изгибом вверх

Точное совместное решение уравнений (1.24) и (1.25) получить достаточно сложно, поэтому для практических задач чаще используют энергетические методы, один из которых в простейшей постановке рассмотрен в разделе 1.1. При решении более сложных задач определяют полную энергию системы 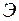, которая равна разности потенциальной энергии деформации 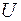и работе внешних сил на возможных перемещениях

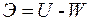. (1.27)

Чтобы составить функционал энергии 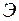для рассматриваемой задачи, необходимо задать форму волны выпучивания трубопровода, подобно выражению (1.16). В работе [2], на основании проведенных исследований было установлено, что начальная форма изгиба трубы и форма, полученная после дополнительных поперечных перемещений 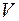, аналогичны и наилучшим образом описываются следующими выражениями

, (1.28)

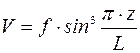, (1.29)

где 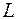– длина волны выпучивания участка трубопровода (рис. 6).

Потенциальная энергия системы труба – грунт, складывается из потенциальной энергии деформации упругоизогнутой трубы (формула 1.10) и потенциальной энергии накапливаемой грунтом при его деформации, которая подобно сжимаемой пружине будет равна половине произведения силы на перемещение для каждого бесконечно малого элемента в соответствии с уравнениями (1.24) и (1.26)

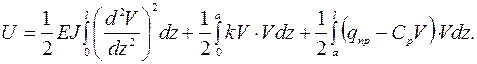
(1.30)

Работа внешних сил совершается продольной силой 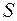только на дополнительных перемещениях 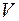и будет вычисляться аналогично формулам (1.13) и (1.14)

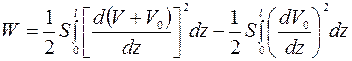. (1.31)

После подстановки в выражения (1.30) и (1.31) уравнений начального и дополнительного прогибов (1.28), (1.29) и интегрирования получается выражение для полной энергии системы трубопровод – грунт

(1.32)

Условию равновесия этой системы соответствует равенство нулю первой вариации полной энергии на возможных перемещениях. Для данной задачи первая вариация будет равна частной производной по дополнительной стрелке прогиба трубопровода 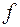, которая полностью определяет форму дополнительных перемещений 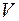в соответствии с выражением (1.29)

. (1.33)

Подробный анализ получаемой в результате таких исследований информации приводится в работе [2]. Наиболее важная зависимость между полным прогибом трубопровода 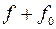и продольным усилием 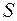качественно представлена диаграммой на рисунке 7. На этой диаграмме полному прогибу 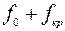соответствует точка потери устойчивости трубопровода второго рода, которая характеризуется неизменностью формы прогиба и наличием максимального продольного усилия, которое называется критическим

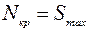. (1.34)

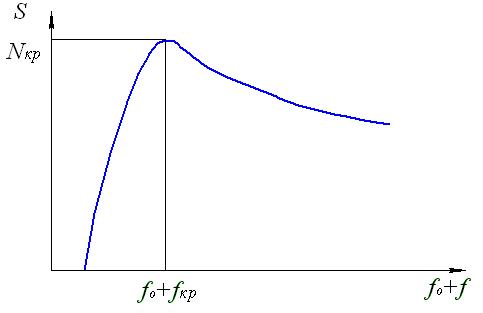
Рис. 7. Диаграмма зависимости полного прогиба трубопровода

от продольного усилия

1.5. Упрощенные зависимости для практических расчетов

Для практических расчетов на устойчивость трубопроводов обычно используются более простые приближенные методики с допущениями, идущими в запас прочности. В данном учебном пособии приводятся рекомендации Всесоюзного научно-исследовательского института по строительству и эксплуатации трубопроводов (ВНИИСТ) [2]. В них предложены формулы для проверки условия устойчивости в соответствии с требованиями СНиП 2.05.06-85 «Магистральные трубопроводы»

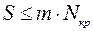, (1.35)

где 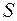– продольное сжимающее усилие;

– коэффициент условий работы магистрального трубопровода;

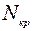– критическая сжимающая сила.

Далее приводятся формулы для двух наиболее важных расчетных схем подземного трубопровода:

· прямолинейный участок;

· изогнутый вверх участок.

1.5.1. Расчет на устойчивость прямолинейного участка трубопровода

Формулы для прямолинейного участка применяются в тех случаях, когда расчетный радиус изгиба 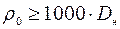(рис. 6).

Критическая продольная сила заглубленного в грунт трубопровода

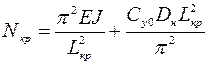, (1.36)

где 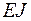– изгибная жесткость трубы.

Расчетная длина волны выпучивания, соответствующая минимальному значению критического усилия

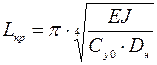. (1.37)

Продольное сжимающее усилие

, (1.38)

где 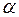– температурный коэффициент линейного расширения;

– температурный перепад;

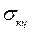– кольцевые напряжения от внутреннего давления.

1.5.2. Расчет на устойчивость изогнутого вверх участка трубопровода

Критическая продольная сила

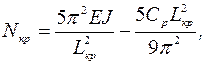(1.39)

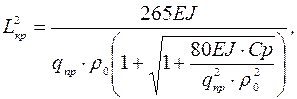(1.40)

где – расчетный радиус оси изгиба трубопровода.

С учетом связи межу расчетным радиусом оси изгиба и критической длины волны выпучивания 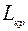значение критической продольной силы можно определить по простой формуле

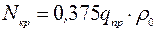. (1.41)

Дополнительная стрела прогиба, соответствующая потере устойчивости:

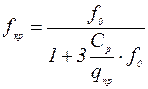, (1.42)

. (1.43)

При расчетном радиусе продольное сжимающее усилие 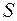вычисляется с учетом самокомпенсации (податливости) изогнутого участка трубопровода и продольных перемещений примыкающих прямолинейных участков. Прежде чем получить выражения для продольной силы 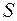необходимо ввести несколько параметров, зависящих от геометрических и механических характеристик рассматриваемой системы

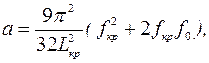(1.44)

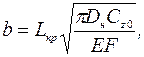(1.45)

где 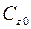- обобщенный коэффициент касательного сопротивления грунта.

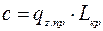, (1.46)

где 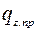– предельное сопротивление грунта сдвигу.

Так как примыкающая часть прямолинейного трубопровода получает продольные перемещения, то возможны два случая его взаимодействия с грунтом и соответственно разные формулы для определения продольного сжимающего усилия.

· Участок предельного равновесия грунта отсутствует. В этом случае выполняется критерий

. (1.47)

В этом случае сжимающее усилие имеет следующий вид

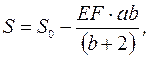(1.48)

· Имеется участок предельного равновесия грунта. Этому случаю соответствуют критерий

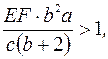(1.49)

и сжимающая сила

. (1.50)