 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Расчет элементов строительных конструкций на сжатие
|
|
При расчете элементов строительных конструкций на сжатие используется метод расчета на устойчивость при помощи коэффициента уменьшения основного допускаемого напряжения  .
.
Из курса сопротивления материалов известно, что критическая сила, сжимающая прямой стержень, вычисляется с помощью формулы Эйлера
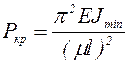 , (6.1)
, (6.1)
где 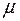 – коэффициент приведенной длины, зависящий от условий закрепления стержня.
– коэффициент приведенной длины, зависящий от условий закрепления стержня.
Зная критическую силу, вычисляют критическое напряжение и условие применимости формулы Эйлера
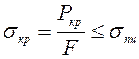 , (6.2)
, (6.2)
где  - предел пропорциональности стали.
- предел пропорциональности стали.
Подставив выражение для критической силы, получаем
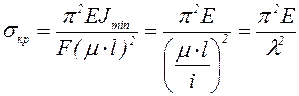 , (6.3)
, (6.3)
где  – радиус инерции сечения;
– радиус инерции сечения;
 – гибкость стержня.
– гибкость стержня.
Таким образом, критическое напряжение зависит только от модуля упругости  и гибкости стержня
и гибкости стержня 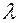 .
.
Если 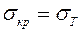 , а для хрупких материалов
, а для хрупких материалов 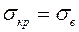 , то этим напряжениям соответствует гибкость
, то этим напряжениям соответствует гибкость 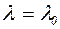 .
.
Стержни, у которых гибкость 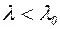 называются стержнями малой гибкости. В этом случае сжатые элементы рассчитывают только на прочность.
называются стержнями малой гибкости. В этом случае сжатые элементы рассчитывают только на прочность.
В случае стержней большой гибкости опасным состоянием следует считать момент возникновения в сжатом стержне напряжения  .
.
Условие работоспособности сжатого стержня 
На практике критическое напряжение вычисляют в зависимости от расчетного сопротивления
 , (6.4)
, (6.4)
где  – коэффициент продольного изгиба (коэффициент уменьшения допускаемого напряжения на сжатие). Его определяют в зависимости от гибкости
– коэффициент продольного изгиба (коэффициент уменьшения допускаемого напряжения на сжатие). Его определяют в зависимости от гибкости 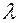 , расчетного сопротивления
, расчетного сопротивления  и модуля упругости (модуля Юнга)
и модуля упругости (модуля Юнга)  .
.
6.1. Расчет центрально сжатых колонн
Центрально сжатыми называются колонны, нагруженные сжимающими силами, направленными вдоль оси колонны (рис. 41). Такие колонны необходимо рассчитывать на прочность и устойчивость.
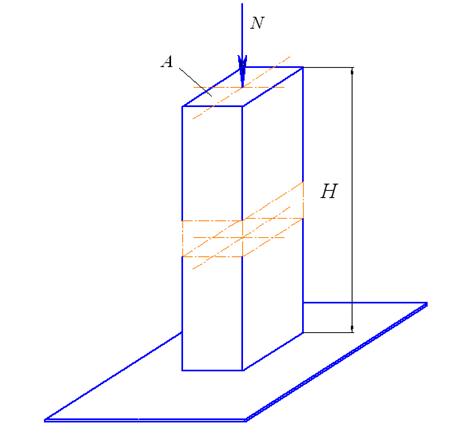
Рис 41. Центрально сжатая колонна
Условие прочности отражает первое предельное состояние
 , (6.5)
, (6.5)
где  – сжимающая сила;
– сжимающая сила;
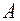 – площадь сечения колонны.
– площадь сечения колонны.
Условие устойчивости формулируется с использованием коэффициента продольного изгиба  (уменьшения допускаемого напряжения на сжатие)
(уменьшения допускаемого напряжения на сжатие)
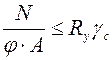 . (6.6)
. (6.6)
Коэффициент  определяется в зависимости от гибкости колонны
определяется в зависимости от гибкости колонны
 , (6.7)
, (6.7)
где  – расчетная длина колонны, которая принимается равной высоте колонны;
– расчетная длина колонны, которая принимается равной высоте колонны;
 – радиус инерции поперечного сечения.
– радиус инерции поперечного сечения.
При вычислении гибкости колонны коэффициент приведенной длины принимается как для случая шарнирного закрепления по концам колонны, т.е. 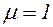 . Такое условие можно принять для случая свободного опирания траверсы, несущей трубопроводы, на колонну сверху и полагая, что соединение базы колонны с фундаментом не создает защемления нижнего конца колонны в силу того, что существует возможность изгиба опорной плиты.
. Такое условие можно принять для случая свободного опирания траверсы, несущей трубопроводы, на колонну сверху и полагая, что соединение базы колонны с фундаментом не создает защемления нижнего конца колонны в силу того, что существует возможность изгиба опорной плиты.
Коэффициент  вычисляют в зависимости от величины условной гибкости колонны
вычисляют в зависимости от величины условной гибкости колонны
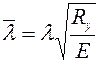 . (6.8)
. (6.8)
Значения j следует определять по формулам СНиП II-23-81
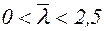
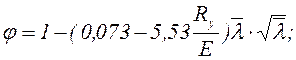 (6.9)
(6.9)

 (6.10)
(6.10)
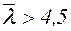
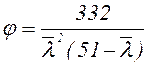 . (6.11)
. (6.11)
При этом гибкость колонны не должна превышать предельной гибкости
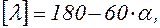 (6.12)
(6.12)
где
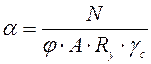 a – коэффициент, принимаемый не менее 0,5.
a – коэффициент, принимаемый не менее 0,5.
Исходя из условия предельной гибкости, можно рекомендовать предельные размеры при проектировании колонн.
Так, например, для сварных двутавровых колонн принимается:
· толщина листов для поясов двутавра 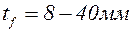 ;
;
· толщина листов для стенки двутавра 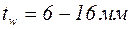 .
.
Высоту двутаврового сечения (рис. 42) принимают в зависимости от высоты колонны
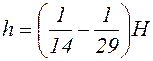 . (6.13)
. (6.13)

Рис 42. Обозначение размеров поперечного сечения двутавра
Для соотношения геометрических размеров поперечного сечения в зависимости от гибкости
 (6.14)
(6.14)
 (6.15)
(6.15)
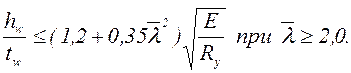 (6.16)
(6.16)
Для укрепления контура сечения и стенки колонны, при отношении 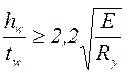 , устанавливают парные поперечные ребра жесткости на расстоянии 2,5-3 м, но не менее 2-х на одном отправочном элементе.
, устанавливают парные поперечные ребра жесткости на расстоянии 2,5-3 м, но не менее 2-х на одном отправочном элементе.
Если в результате расчета требуется вычислить площадь поперечного сечения  но в этом случае коэффициент продольного изгиба
но в этом случае коэффициент продольного изгиба  не известен, поскольку он сам зависит от площади поперечного сечения.
не известен, поскольку он сам зависит от площади поперечного сечения.
Для разрешения этого противоречия используется метод последовательных приближений для подбора коэффициента  . Первоначально можно принять
. Первоначально можно принять  . После этого вычисляют площадь сечения
. После этого вычисляют площадь сечения 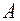 и уже для этой величины площади подбирают размеры сечения. Установив размеры поперечного сечения колонны и определив геометрические характеристики
и уже для этой величины площади подбирают размеры сечения. Установив размеры поперечного сечения колонны и определив геометрические характеристики  ,
,  и
и 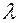 , устанавливают фактическое значение
, устанавливают фактическое значение  .
.
При второй попытке 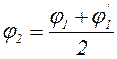 и т.д. пока не выполнится условие
и т.д. пока не выполнится условие 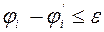 , где
, где 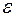 наперед заданная малая величина.
наперед заданная малая величина.
6.2. Расчет внецентренно сжатых колонн
В том случае, когда линия действия сжимающей силы не совпадает с осью колонны, в поперечных сечениях колонны кроме продольной силы возникает изгибающий момент (рис. 43).

Рис. 43. Внецентренно сжатая колонна.
Тогда в случае изгиба в одной плоскости условие прочности запишется следующим образом
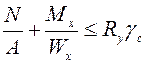 . (6.17)
. (6.17)
А при изгибе в 2-х плоскостях
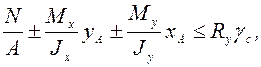 (6.18)
(6.18)
где  – координаты наиболее опасной точки.
– координаты наиболее опасной точки.
Устойчивость колонны в плоскости действия изгибающего момента 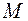 проверяют с учетом коэффициента
проверяют с учетом коэффициента 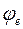 , который зависит от гибкости колонны
, который зависит от гибкости колонны
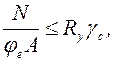 (6.19)
(6.19)
где  – продольная сила, приложенная с эксцентриситетом
– продольная сила, приложенная с эксцентриситетом 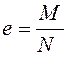 ;
;
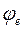 – коэффициент устойчивости, определяемый в зависимости от условной гибкости
– коэффициент устойчивости, определяемый в зависимости от условной гибкости
 , (6.20)
, (6.20)
где 
и приведенного относительного эксцентриситета
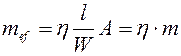 , (6.21)
, (6.21)
где 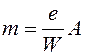 относительный эксцентриситет;
относительный эксцентриситет;
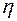 – коэффициент влияния формы сечения, который для двутавра определяется (таб. 6.1) в зависимости от
– коэффициент влияния формы сечения, который для двутавра определяется (таб. 6.1) в зависимости от  ,
, 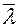 и отношения
и отношения 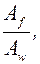
где  – площадь полки двутавра;
– площадь полки двутавра;
 – площадь стенки двутавра.
– площадь стенки двутавра.
Таблица 6.1

| 
| ||
0≤ 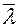 ≤5 ≤5
| 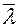 >5 >5
| ||
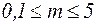
| 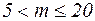
| 
| |
| 0,25 | (1,45-0,05)-0,01(5-  ) ) 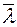
| 1,2 | 1,2 |
| 0,5 | (1,75-0,1)-0,02(5-  ) ) 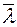
| 1,25 | 1,25 |
| ≥1,0 | (1,90-0,1)-0,02(6-m) 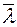
| 1,4-0,02 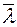
| 1,3 |
Для других сечений коэффициент  определяется по таблице 73 (СНиП II-23-81).
определяется по таблице 73 (СНиП II-23-81).
Коэффициенты je для проверки устойчивости внецентренно-сжатых сплошностенчатых стержней в плоскости действия момента, совпадающей с плоскостью симметрии, определяется по таблице 74 (СНиП II-23-81). В таблице 6.2 приведены некоторые значения je.
Таблица 6.2
Условная гибкость 
| Коэффициент je при приведенном относительном эксцентриситете mеf | |||||||||
| 0,1 | 1,0 | 2,0 | 4,0 | 6,0 | 8,0 | 10,0 | 14,0 | 20,0 | ||
| 0,5 | 0,967 | 0,722 | 0,538 | 0,337 | 0,237 | 0,210 | 0,150 | 0,106 | 0,077 | |
| 1,0 | 0,925 | 0,653 | 0,484 | 0,307 | 0,225 | 0,196 | 0,142 | 0,103 | 0,074 | |
| 2,0 | 0,813 | 0,536 | 0,397 | 0,260 | 0,193 | 0,170 | 0,125 | 0,094 | 0,067 | |
| 4,0 | 0,505 | 0,330 | 0,256 | 0,181 | 0,140 | 0,127 | 0,098 | 0,078 | 0,057 | |
| 6,0 | 0,258 | 0,198 | 0,166 | 0,128 | 0,104 | 0,096 | 0,079 | 0,066 | 0,049 | |
| 8,0 | 0,152 | 0,128 | 0,113 | 0,091 | 0,078 | 0,074 | 0,062 | 0,053 | 0,041 | |
| 1,0 | 0,100 | 0,090 | 0,079 | 0,069 | 0,059 | 0,057 | 0,049 | 0,043 | 0,035 |
Колонну необходимо также проверить на возможность потери усточивости из плоскости действия изгибающего момента по формуле:
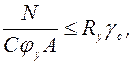 (6.22)
(6.22)
где 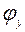 – коэффициент продольного изгиба колонны в зависимости от условной гибкости
– коэффициент продольного изгиба колонны в зависимости от условной гибкости
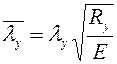 . (6.23)
. (6.23)
Коэффициент 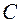 вычисляется в cоответствии с пунктом 5.31 СНиП II-23-81.
вычисляется в cоответствии с пунктом 5.31 СНиП II-23-81.
6.3. Расчет базы колонны
Рассмотрим расчет базы колонны на примере сварной двутавровой колонны (рис 44).
Вначале определяется требуемая площадь опорной плиты из условия отсутствия смятия бетона
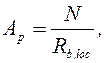 (6.24)
(6.24)
где 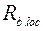 – расчетное сопротивление бетона смятию
– расчетное сопротивление бетона смятию
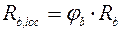 ,
, 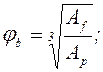
 ;
;
 – площадь опорной плиты колонны;
– площадь опорной плиты колонны;
 – площадь верхнего обреза фундамента.
– площадь верхнего обреза фундамента.

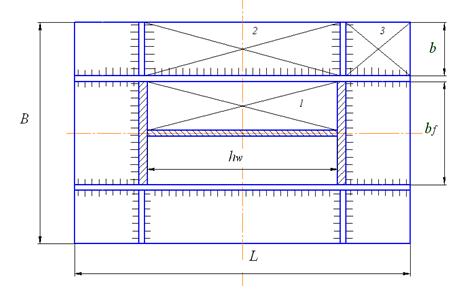
Рис. 44. База колонны
Расчетное сопротивление бетона сжатию (таблица 6.3)
Таблица 6.3
| Класс прочности | В7,5 | В10 | В12 | В15 | В20 |
| Расчетное сопротивление, МПа | 4,5 | 6,0 | 7,5 | 8,5 | 11,5 |
В первом приближении принимают 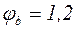 .
.
Ширина опорной плиты
 , (6.25)
, (6.25)
где  – ширина пояса двутавровой колонны;
– ширина пояса двутавровой колонны;
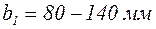 .
.
Длина опорной плиты 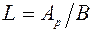 .
.
При расчете на прочность опорной плиты используются известные решения для прямоугольных пластин. При этом вся плита разбивается на отдельные участки, т.е. на отдельные пластинки, границами которых служат конструктивные элементы базы колонны, которыми она опирается на опорную плиту.
В соответствии с рис. 45 можно выделить несколько характерных вариантов плиты с различными условиями на ее границах. Для каждого варианта закрепления плиты вычисляется максимальный изгибающий момент.
Вариант 1. Плита оперта по 4-м сторонам (рис. 45, 1)

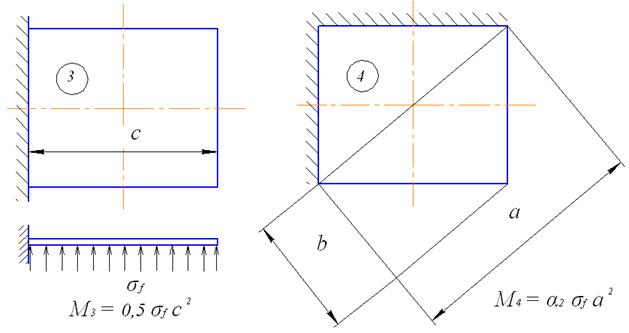
Рис. 45. Расчетные схемы опорной плиты базы колонны
 , (6.26)
, (6.26)
где 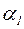 и
и  коэффициенты, величина которых зависит от отношения
коэффициенты, величина которых зависит от отношения 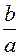 ;
;
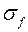 – реактивное давление фундамента на опорную плиту;
– реактивное давление фундамента на опорную плиту;
 – конструктивные элементы.
– конструктивные элементы.
Вариант 2. Плита оперта по 3-м сторонам (рис. 45, 2)
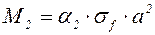 . (6.27)
. (6.27)
Вариант 3. Консольная плита (рис. 5.43, 3)
 . (6.28)
. (6.28)
Вариант 4. Плита, опертая по 2-м сторонам (рис. 45, 4)
 . (6.29)
. (6.29)
Для этого варианта под обозначением 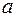 понимается диагональ прямоугольника, а
понимается диагональ прямоугольника, а  – расстояние от вершины угла до диагонали.
– расстояние от вершины угла до диагонали.
Коэффициенты для расчета плит на изгиб.
Таблица 6.4
| Плиты опертые по 4-м сторонам | Опертые по 3-м сторонам | ||

| 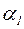
| 
| 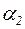
|
| 1,0 1,2 1,4 1,6 1,8 ≥2,0 | 0,048 0,063 0,075 0,086 0,094 0,125 | 0,5 0,7 0,9 1,2 1,4 2,0 ≥2,0 | 0,060 0,088 0,107 0,120 0,126 0,132 0,133 |
Толщину опорной плиты определяют по наибольшему изгибающему моменту из найденных для различных участков
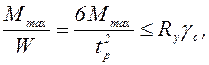 (6.30)
(6.30)
где 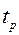 - толщина опорной плиты.
- толщина опорной плиты.
Тогда условие прочности для толщины опорной плиты
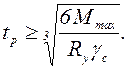 (6.31)
(6.31)
Продольное усилие  передается от колонны на траверсу при помощи 4-х сварных швов.
передается от колонны на траверсу при помощи 4-х сварных швов.
Если задать катет 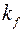 можно найти требуемую высоту траверсы.
можно найти требуемую высоту траверсы.
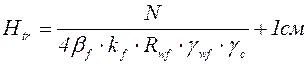 . (6.32)
. (6.32)
Толщина листов траверсы и ребер жесткости принимается равной 12-16 мм.
Катет сварных швов, прикрепляющих листы траверсы и ребра жесткости к опорной плите
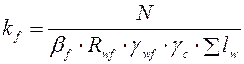 , (6.33)
, (6.33)
где  .
.
Диаметр анкерных монтажных болтов принимают без расчета равным 20-30мм.
Дата публикования: 2014-09-25; Прочитано: 6892 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
