 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пример.Для вычисления воспользуемся замечательными пределами а) и д)
|
|
Действительно, 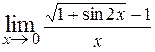 = =
= =  = =
= =  = =
= = 
 .
.
Обозначим  при
при 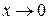 .
.
Тогда получим 2 
 = 2
= 2  = =
= =  , так как
, так как  = 1.
= 1.
Если требуется вычислить  а
а  ,
,  =
=  тогда говорят, что имеет место неопределённость типа
тогда говорят, что имеет место неопределённость типа  . Для раскрытия такой неопределённости используется замечательный предел б).
. Для раскрытия такой неопределённости используется замечательный предел б).
Пример. Вычислим  . Так как
. Так как  = 1, а 1–
= 1, а 1–  при
при  ,
,
то имеет место неопределённость типа  .
.
Далее,  = 1 +
= 1 +  .
.
Обозначим  при
при  .
.
Тогда  , а
, а  . Данный предел примет вид
. Данный предел примет вид  =1+ аат место неопределённо (
=1+ аат место неопределённо ( =
=  =
=  , так как
, так как 
 .
.
Задание 9. Это контрольное задание относится к теме: «Непрерывность функции, точки разрыва и их классификация». Рассмотрим основные понятия, относящиеся к этой теме.
Определение. Функция  называется непрерывной в точке
называется непрерывной в точке 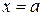 , если: 1)
, если: 1)  определена в некоторой окрестности точки
определена в некоторой окрестности точки  (то есть можно вычислить значения функции для всех значений
(то есть можно вычислить значения функции для всех значений 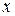
 (
( – δ,
– δ,  + δ), где δ есть некоторое положительное число); 2)существует
+ δ), где δ есть некоторое положительное число); 2)существует 
 =
=  .
.
Если функция  непрерывна в каждой точке множества X, тогда говорят, что функция
непрерывна в каждой точке множества X, тогда говорят, что функция  непрерывна на множестве X.
непрерывна на множестве X.
Определение. Точка 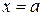 называется точкой разрыва функции
называется точкой разрыва функции  , если
, если  не является непрерывной в этой точке.
не является непрерывной в этой точке.
Из определения точки разрыва следует, что если  не определена в точке
не определена в точке  , тогда точка
, тогда точка  является точкой разрыва этой функции. Например, функция
является точкой разрыва этой функции. Например, функция  =
=  не определена в точке
не определена в точке  0, следовательно,
0, следовательно,  0 является точкой разрыва этой функции.
0 является точкой разрыва этой функции.
Из определения также следует, что 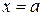 является точкой разрыва функции, если не выполняется условие 2) определения непрерывности. Развернём подробнее условие 2), используя понятие односторонних пределов. Левосторонний и правосторонний пределы функции
является точкой разрыва функции, если не выполняется условие 2) определения непрерывности. Развернём подробнее условие 2), используя понятие односторонних пределов. Левосторонний и правосторонний пределы функции  при
при 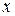 →
→  обозначают так:
обозначают так: 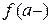 ,
, 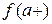 и, по определению,
и, по определению, 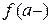 =
= 
 (
(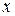 стремится к
стремится к  , оставаясь меньше
, оставаясь меньше  ),
), 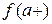 =
= 
 (
(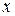 стремится к
стремится к  , оставаясь больше
, оставаясь больше  ). Условие 2) будет равносильно следующему условию: существуют односторонние пределы
). Условие 2) будет равносильно следующему условию: существуют односторонние пределы 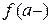 ,
, 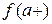 и выполняются равенства
и выполняются равенства 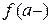 =
= 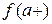 =
=  . Следовательно, точка
. Следовательно, точка 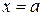 будет точкой разрыва, если хотя бы одно из условий 2) не будет выполнено.
будет точкой разрыва, если хотя бы одно из условий 2) не будет выполнено.
Определение. Точка 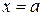 называется точкой разрыва первого рода функции
называется точкой разрыва первого рода функции  , если существуют односторонние пределы
, если существуют односторонние пределы 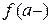 ,
, 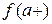 и
и 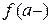 ≠
≠ 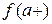 либо
либо 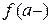 =
= 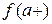 ≠
≠  . При этом число
. При этом число 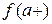 –
– 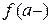 называют скачком функции
называют скачком функции  в точке
в точке 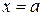 .
.
Определение. Точка 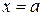 называется точкой разрыва второго рода функции
называется точкой разрыва второго рода функции  , если хотя бы один из односторонних пределов
, если хотя бы один из односторонних пределов 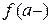 ,
, 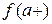 не существует или равен бесконечности.
не существует или равен бесконечности.
Пример. Функция  не определена в точке
не определена в точке  0, а значит,
0, а значит,  0 является точкой разрыва этой функции. Чтобы выяснить тип точки разрыва, вычислим односторонние пределы
0 является точкой разрыва этой функции. Чтобы выяснить тип точки разрыва, вычислим односторонние пределы 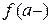 ,
, 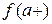 . Так как
. Так как  , а
, а  , если
, если  , то имеем
, то имеем  =
= 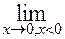

 = 1. Аналогично, так как
= 1. Аналогично, так как  , а
, а  , если
, если  , то
, то  = =
= = 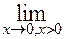
 = 0.
= 0.
Следовательно, точка  0 является точкой разрыва первого рода данной функции, так как 1=
0 является точкой разрыва первого рода данной функции, так как 1=  ≠
≠  = 0. Скачок функции в этой точке равен
= 0. Скачок функции в этой точке равен  –
–  = 0 – 1 = – 1.
= 0 – 1 = – 1.
Пример.  =
= 
Проверим непрерывность этой функции в точке  0. Так как существует (первый замечательный предел)
0. Так как существует (первый замечательный предел) 
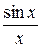 =1, тогда, по теореме об односторонних пределах, существуют односторонние пределы
=1, тогда, по теореме об односторонних пределах, существуют односторонние пределы  ,
,  и справедливы следующие равенства
и справедливы следующие равенства  =
=  =
= 
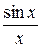 = 1 ≠ 0 =
= 1 ≠ 0 = 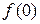 .
.
Следовательно, точка  0 является точкой разрыва первого рода рассматриваемой функции, так как
0 является точкой разрыва первого рода рассматриваемой функции, так как  =
=  = 1 ≠ 0 =
= 1 ≠ 0 = 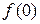 .
.
Пример.  =
=  . Рассматриваемая функция не определена в точке
. Рассматриваемая функция не определена в точке  0, а значит
0, а значит  0 – точка разрыва
0 – точка разрыва  . Вычислим односторонние пределы
. Вычислим односторонние пределы  ,
,  . Имеем,
. Имеем,  =
= 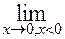
 = 0,
= 0,  =
= 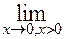
 =
=
= +∞.
Так как правосторонний предел  = +∞, то точка
= +∞, то точка  0 является
0 является
точкой разрыва второго рода.
Выделим теперь основной класс непрерывных функций. Справедливо утверждение, что все элементарные функции (степенная  , показательная
, показательная  , логарифмическая
, логарифмическая  ,
, 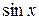 ,
,  ,
, 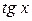 ,
,  ,
,  ,
,  ,
,  ,
,  ) непрерывны в своей области определения. Например, функция
) непрерывны в своей области определения. Например, функция  определена на множестве (0, +∞), а значит и непрерывна на этом множестве.
определена на множестве (0, +∞), а значит и непрерывна на этом множестве.
Перечислим основные свойства непрерывных функций. Пусть функции  и
и 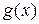 непрерывны в точке
непрерывны в точке 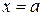 .
.
Тогда: 1) функция C  , где C есть постоянная, непрерывна в точке
, где C есть постоянная, непрерывна в точке 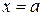 ; 2)
; 2)  +
+ 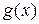 непрерывна в точке
непрерывна в точке 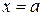 ; 3)
; 3) 
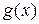 непрерывна в точке
непрерывна в точке 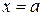 ; 4)
; 4)  непрерывна в точке
непрерывна в точке 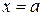 , если
, если  ≠ 0; 5) непрерывность суперпозиции двух функций (сложной функции): если функция
≠ 0; 5) непрерывность суперпозиции двух функций (сложной функции): если функция 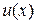 непрерывна в точке
непрерывна в точке 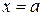 ,
,  = =
= =  , а функция
, а функция  непрерывна в точке
непрерывна в точке  , тогда функция
, тогда функция 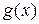 = =
= =  непрерывна в точке
непрерывна в точке 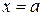 .
.
Из непрерывности основных элементарных функций и свойств непрерывных функций следует, что сумма, произведение и частное двух элементарных функций непрерывна в своей области определения. Например, функция 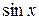 +
+  непрерывна на множестве (0, +∞); функция
непрерывна на множестве (0, +∞); функция  непрерывна в своей области определения (0,+∞) как частное двух элементарных функций. Функция
непрерывна в своей области определения (0,+∞) как частное двух элементарных функций. Функция  определена на промежутке (–1, 1), а значит и непрерывна на этом промежутке.
определена на промежутке (–1, 1), а значит и непрерывна на этом промежутке.
Пример. Исследовать на непрерывность функцию
 =
= 
Отметим, что во всех точках, кроме точек  1,
1,  3, функция непрерывна как элементарная функция. Точки
3, функция непрерывна как элементарная функция. Точки  1,
1,  3 могут быть точками разрыва потому, что слева и справа от них функция задаётся разными аналитическими выражениями, а именно,
3 могут быть точками разрыва потому, что слева и справа от них функция задаётся разными аналитическими выражениями, а именно,  =
= 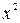 для
для 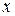 < 1 и
< 1 и  =
=  для
для 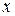 > 1. Вычислим односторонние пределы в этих точках. Имеем,
> 1. Вычислим односторонние пределы в этих точках. Имеем, 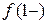 =
= 
 =
=  = 1,
= 1, 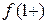 =
= 
 = =
= = 
 = 1,
= 1,  = 2 ─ 1= 1.
= 2 ─ 1= 1.
Следовательно, 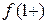 =
= 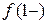 =
=  = 1, а значит, рассматриваемая функция непрерывна в точке
= 1, а значит, рассматриваемая функция непрерывна в точке  1. Для точки
1. Для точки  3 имеем,
3 имеем,  =
= 
 =
=  = –1,
= –1,  =
= 
 = =
= =  = 1, а
= 1, а  = 2 – 3= –1.
= 2 – 3= –1.
Следовательно,  ≠
≠  и точка
и точка  3 является точкой разрыва первого рода рассматриваемой функции.
3 является точкой разрыва первого рода рассматриваемой функции.
Задание 10. Это задание относится к теме: «Дифференциальное исчисление функции одной переменной». Основным понятием этой темы является понятие производной функции.
Определение. Производной функции  в точке
в точке  называется число
называется число 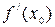 =
=  , если этот предел существует; если в точке
, если этот предел существует; если в точке  существует производная
существует производная 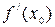 , тогда говорят, что функция
, тогда говорят, что функция  дифференцируема в точке
дифференцируема в точке  ; если функция
; если функция  дифференцируема на множестве X, то функция
дифференцируема на множестве X, то функция  называется дифференцируемой на множестве X.
называется дифференцируемой на множестве X.
Разность 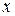 –
–  называют приращением аргумента, а разность
называют приращением аргумента, а разность  ––
–– 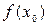 называют приращением функции, соответствующим приращению аргумента
называют приращением функции, соответствующим приращению аргумента 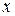 –
–  . Если обозначить приращение аргумента ∆
. Если обозначить приращение аргумента ∆ 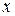 =
= 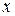 –
–  , тогда производная, в эквивалентной форме, определится так
, тогда производная, в эквивалентной форме, определится так 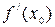 = =
= =  .
.
Вычислим производную функции  =
=  в точке
в точке 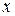 . По определению имеем,
. По определению имеем, 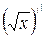 =
=  =
=  = =
= =  =
=  =
=  .
.
Из определения производной функции и замечательных пределов получают производные основных элементарных функций.
Таблица производных основных элементарных функций
1.  =
= 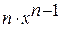 (производная степенной функции);
(производная степенной функции);
2.  =
= 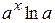 (производная показательной функции), в частности
(производная показательной функции), в частности  =
=  ;
;
3.  = =
= =  (производная логарифмической функции), в частности
(производная логарифмической функции), в частности  =
=  ;
;
4.  =
=  ;
;
5.  =
= 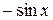 ;
;
6.  =
=  ;
;
7.  = =
= =  ;
;
8.  =
=  ;
;
9.  =
=  ;
;
10.  =
=  ;
;
11.  =
=  .
.
Например, чтобы вычислить производную функции  ,
,
применяем пункт 1 таблицы и получаем  .
.
Правила дифференцирования. Пусть функции 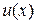 ,
,  дифференцируемы в точке
дифференцируемы в точке 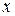 , тогда справедливы равенства 1 – 4:
, тогда справедливы равенства 1 – 4:
1. (c)′ = 0 (производная постоянной величины равна нулю);
2. (c  )′ = c
)′ = c  ′ (постоянный множитель можно вынести за знак производной);
′ (постоянный множитель можно вынести за знак производной);
3. ( )′ =
)′ =  ′ +
′ + 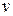 ′ (производная суммы равна сумме производных);
′ (производная суммы равна сумме производных);
4. ( )′ =
)′ =  ′
′ 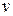 +
+ 
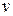 ′ (производная произведения двух функций);
′ (производная произведения двух функций);
5.  (производная частного двух функций).
(производная частного двух функций).
6. Дифференцирование сложной функции: если функция 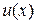 дифференцируема в точке
дифференцируема в точке 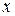 ,
,  =
= 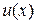 , а функция
, а функция  дифференцируема в точке
дифференцируема в точке  , тогда функция
, тогда функция 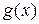 =
=  дифференцируема в точке
дифференцируема в точке 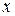 и справедливо равенство
и справедливо равенство 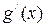 =
= 
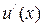 .
.
Пример. Пусть 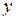 = 2 +
= 2 +  .
.
Вычислим  . Из правил дифференцирования и таблицы производных получаем, что
. Из правил дифференцирования и таблицы производных получаем, что  = (2)′ + +
= (2)′ + +  – (
– ( )′ +
)′ +  = 0 + (
= 0 + (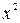 )′
)′  +
+  –
–  + +
+ +  =
=  –
–  +
+  =
=
= 
 +
+ 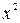
 –
–  +
+  =
= 
 +
+ 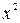
 –
–  + +
+ + 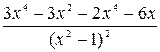 =
= 
 +
+ 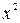
 –
–  +
+  .
.
Дата публикования: 2014-10-20; Прочитано: 399 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
