И плотность распределения вероятностей

Пусть случайная величина задана тройкой ( , Â, P ). Будем обозначать случайные величины греческими буквами, а значения, которые они принимают – соответствующими латинскими. Например, если случайная величина обозначена буквой x, то значения, которые она принимает, будем обозначать буквой x.

Математическое определение (интегральной) функции распределения непрерывной случайной величины (обычно слово “интегральной” из этого термина опускают): .

Понятно, что эта функция неотрицательна и не убывает на всей оси. Область значений функции распределения – [0, 1]. Пример графика функции распределения непрерывной случайной величины показан на рис. 7 а.

Представим полуоткрытый интервал (-¥, b ], как объединение двух непересекающихся полуоткрытых интервалов:

(-¥, b ] = (-¥, а ] (a, b ].

Тогда в связи с аддитивностью вероятностной меры

= ,

и, по определению функции распределения,

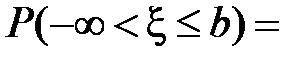F(b) = F (a) + .

Отсюда следует, что = F (b) - F(a).

Механической аналогией, удобной для понимания смысла функции распределения непрерывной случайной величины, может служить ось с переменной плотностью материала, из которого она изготовлена. Тогда механическим аналогом функции распределения может служить зависимость веса левого отрезка оси от координаты разреза. Последнее выражение показывает, что вес отрезка оси, вырезанного из середины, равен разности между весом отрезка (-¥, b ] и отрезка (-¥, a ].

Встав на путь механических аналогий, мы не можем не заинтересоваться такой характеристикой, как удельный вес или плотность материала оси, тем более что плотность изменяется по длине оси, то есть плотность есть функция от x:j(x).

По определению плотности (или удельного веса) бесконечно тонкого стержня,

.

Функция j(x) называется плотностью распределения вероятностей или законом распределения вероятностей непрерывной случайной величины. Она представлена на рис. 7, б). Поскольку функция распределения – неубывающая функция, j(x) 0.

Для плотности распределения справедливы следующие соотношения:

, ,

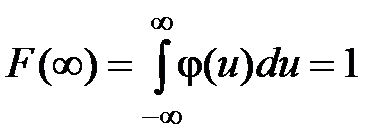где u так же, как x – значения, которые может принимать случайная величина x.

Последнее из этих соотношений является условием нормировки плотности распределения вероятностей.

Вероятность того, что в результате испытания случайная величина примет значение из полуоткрытого интервала (a, b ], то есть вероятностная мера этого интервала, вычисляется как площадь криволинейной трапеции, находящейся под кривой плотности распределения над этим интервалом:

.

Таким образом, площадь под всей кривой плотности распределения есть вероятность достоверного события, которое заключается в том, что в результате испытания случайная величина примет какое-либо значение.

Кроме того, из приведенных соотношений следует, что событие x = с невозможно, поскольку вероятность того, что в результате испытания непрерывная случайная величина примет конкретное значение, равна нулю:

.

Иными словами, это означает, что в условиях, когда определена непрерывная случайная величина, вероятностная мера точки есть нуль.

Отметим, что, хотя точка не является полуоткрытым интервалом, мы имеем право рассматривать вероятностную меру точки, поскольку в классе полуоткрытых интервалов может быть построена бесконечная сходящаяся последовательность, пределом которой является точка, принадлежащая сигма-алгебре Â.