Случайной величины

Характеристической функцией непрерывной случайной величины x называется математическое ожидание случайной функции (см., например, [3, 4]):

.

Иными словами, характеристическая функция случайной величины есть интегральное преобразование плотности распределения этой случайной величины. Это преобразование – частный случай применения обратного преобразования Фурье к функциям, обладающим специфическими свойствами, присущими плотности распределения, а именно к неотрицательным функциям, интеграл от которых по всему множеству их определения равен 1. Отсюда следует, что характеристическая функция и плотность распределения связаны взаимно однозначно, то есть

.

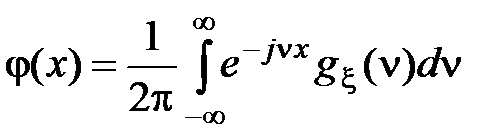Приведем несколько полезных свойств характеристической функции, первое из которых порождено спецификой плотности распределения случайной величины.

a) При n = 0

,

,

................................

................................. .

Эти равенства означают, что для определения начальных моментов всех порядков достаточно знать выражение для характеристической функции, продифференцировать его k раз по аргументу n, подставить в полученную производную значение n = 0и разделить результат на . В частности, если необходимо определить дисперсию, то придется найти первый и второй начальные моменты и затем воспользоваться соотношением, которое было получено в разд. 1.3.3:

.

б) Если задана случайная величина h, которая является линейной функцией случайной величины x:h = a x + b, то характеристическая функция случайной величины h есть

.

Это свойство, в частности, означает, что при простом смещении значений случайной величины по оси абсцисс на величину b характеристическая функция умножается на экспоненту в степени jn b: если h = x + b, то .

в) Пусть имеется последовательность плотностей распределения непрерывных случайных величин. Пусть – характеристические функции этих случайных величин. Если последовательность плотностей распределения сходится и предельная плотность распределения j(x), то последовательность характеристических функций также сходится и имеет предельную функцию g (n), которая есть характеристическая функция случайной величины с предельной плотностью распределения j(x). Иными словами, из сходимости плотностей распределения случайных величин следует сходимость их характеристических функций. Справедливо и обратное утверждение: из сходимости характеристических функций случайных величин следует сходимость их плотностей распределений.

Это свойство очевидным образом следует из взаимно однозначной связи между характеристическими функциями и плотностями распределения.

Необходимые условия того, чтобы некоторая функция g (n)была характеристической функцией:

g (n)непрерывна поn;

g (n) определена на каждом конечном интервалеn;

g (0) = 1;

| g (n)| £ 1.