 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Интегрирование путем подведения под знак дифференциала
|
|
Все формулы таблицы основных интегралов справедливы, когда переменная интегрирования не является независимой, а представляет функцию от некоторой другой переменной:  .
.
Тогда  или
или  .
.
Пример4. Вычислить интеграл 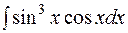 .
.
Решение. Так как  ,
,
то 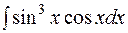 =
=  .
.
Здесь мы применили формулу 1 таблицы интегралов.
Пример5. Вычислить интеграл  .
.
Решение. Заметим, что  , тогда имеем:
, тогда имеем:
 =
=  .
.
Дата публикования: 2014-10-20; Прочитано: 297 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
