 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение. 1. Областью определения функции – вся действительная ось, кроме точки , т.е
|
|
1. Областью определения функции – вся действительная ось, кроме точки 
, т.е. 
, 
.
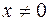2. Найдем производную функции:
.
3. Производная обращается в ноль при 
и 
и не существует в точке , которая не принадлежит области определения функции.
4. Область определения разбивается на следующие интервалы: 
, 
, 
, 
.
5. На промежутке 
. На промежутке 
.На промежутке . На промежутке .
Таким образом, при переходе через точку производная меняет знак с плюса на минус, а это означает, что, в точке функция имеет максимум и 
. Точка не входит в область определения функции и не может быть точкой экстремума. При переходе через точку производная меняет знак с минуса на плюс, поэтому в точке функция имеет минимум и 
. Иллюстрация полученного решения представлена на рис. 2.
Рис. 2
Пример 8. Найти область определения и экстремумы функции 
.
Дата публикования: 2014-10-20; Прочитано: 302 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
