 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Вычисление показателей надежности и риска системы при наличии восстановления
|
|
Предположим, что количество ремонтных органов достаточно для того, чтобы подсистемы были независимы по восстановлению (неограниченное восстановление). В этом случае можно воспользоваться формулами (1.11) и (1.12). Поскольку восстановление элементов значительно повышает надежность системы и снижает риск из-за отказа элементов, то в каждой резервной группе можно оставить лишь по одному резервному элементу. Таким образом, для ремонтируемой системы ее структурная схема имеет вид, показанный на рисунке 5.

Рисунок 5 – Структурная схема восстанавливаемой системы
5.1. Постоянно включенный резерв
Поскольку первая и четвёртая подсистемы являются нерезервированными, а вторая и третья представляют собой дублированные подсистемы, то в соответствии с формулой (1.7) для постоянно включенного резерва получим следующие формулы для вероятности безотказной работы подсистем:

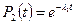 ,,
,,  ,
,  ,
,
где:
 ,
,  ,
,
 ,
,  ,
,
 - интенсивность восстановления элементов
- интенсивность восстановления элементов  -й подсистемы,
-й подсистемы, 

|
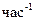
Теперь для вычисления показателей надежности системы можно воспользоваться соотношением (1.11). В результате получим:
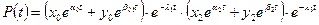 .
.
Расчеты с помощью системы MathCAD показывают, что:

|

|
Аналогично, используя (1.2), найдем риск системы в момент 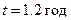 :
:
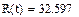
|
5.2. Резерв замещением
В соответствии с формулой (1.9) для резерва замещением получим следующие формулы для вероятности безотказной работы подсистем:
 ,
, 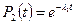 ,
,  ,
,  ,
,
где
 ,
,  ,
,
 ,
,  ,
,
 - интенсивность восстановления элементов
- интенсивность восстановления элементов  -й подсистемы,
-й подсистемы, 
Теперь для вычисления показателей надежности системы можно воспользоваться соотношением (1.11). В результате получим:
 ,
,

|
Расчеты с помощью системы MathCAD показывают, что:

|
Аналогично, используя (1.12), найдем риск системы в момент 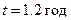 :
:

|
Дата публикования: 2014-10-20; Прочитано: 371 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
