Интегральная предельная теорема Муавра-Лапласа

Пусть производится n независимых испытаний. В каждом испытании возможны два исхода: либо наступит событие A, либо 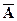. Если вероятность наступления события постоянна и равна р (0<p<1), то при 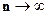для любых a и b:

,

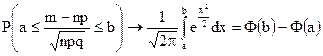где 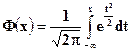- функция Лапласа.

Эта теорема применяется при вычислении вероятностей .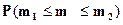

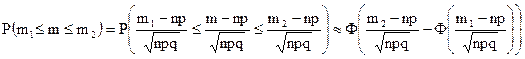. (32)

Пример 16. В страховой компании застраховано 10000 автомобилей. Вероятность поломки любого автомобиля в результате аварии равна 0,006. Каждый владелец застрахованной машины платит в год 12 грн. страховых и в случае ее поломки в результате аварии получает от компании 1000 грн. Найти вероятность того, что по истечении года работы компания потерпит убыток.

Событие A – компания потерпит убыток, n = 10000, p(A) = 0,006, q = 0,994.

Ежегодно кампания получает от клиентов S= 10000*12=120000 грн.

Обозначим m – число автомобилей, потерпевших аварию.

Тогда компания должна выплатить сумму, равную

R = m 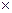1000 грн.

Требуется найти Р(А) = P(R > S) = P(1000m > 120000) = P(m>120).

Перейдем к противоположному событию Ā – компания не потерпит убытки, и найдем вероятность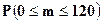

Применим интегральную теорему Муавра-Лапласа

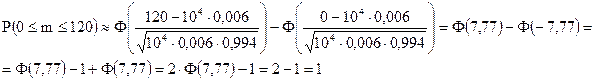
Таким образом, P(A) = 1-Р(Ā) = 1 - 1=0, т.е. вероятность того, что компания потерпит убыток равна нулю.