Многомерные случайные величины

На одном и том же пространстве элементарных исходов можно рассматривать не одну, а несколько случайных величин. Например, подбрасывают три игральных кубика. Можно рассматривать одну случайную величину ξ – сумма выпавших очков или три случайных величины:

ξ₁ – число выпавших очков на 1-ом кубике,

ξ₂ – число выпавших очков на 2-ом кубике,

ξ₃ – число выпавших очков на 3-ем кубике.

В экономике, как правило, на показатель действует несколько факторов, например, качество продукции зависит от многих факторов.

Пусть ξ₁, ξ₂, …, ξ_n –система случайных величин, определенных на множестве .

Функция распределения системы случайных величин определяется формулой

F(x₁, x₂, …, x_n) = P(ξ₁ <x₁, ξ₂ <x₂,..., ξ_n <x_n), (20)

где x₁, x₂, …, x_n ()

При этом F(x₁, x₂, …, x_n) – неубывающая функция каждого аргумента.

Для дискретной системы случайной величины закон распределения определяется заданием вектора x₁, x₂, …,x_n и вектора вероятностей

,

таких, что .

Функция распределения выражается в виде кратной суммы

F(x₁, x₂, …, x_n) = , (21)

где суммирование производится по всем возможным значениям каждой из случайных величин, для которых .

Система ξ₁, ξ₂, …, ξ_n называется непрерывной,если существует

f(x₁, x₂, …, x_n) 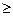0 такая, что для любых x₁, x₂, …, x_nфункцию распределения

F(x) можно представить в виде n-мерного интеграла

F(x) = . (22)

Функция f ( 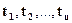) называется плотностью распределения вероятностей системы случайных величин,

f() = (23)

в точках непрерывности.

случайные величины ξ₁, ξ₂, …, ξ_n называются независимыми, если для любых

x₁, x₂, …, x_nнезависимы события .

Для не зависимых ξ₁, ξ₂, …, ξ_n функция распределения равна произведению

функций распределения каждой случайной величины

F(x₁, x₂, …, x_n) = . (24)

Также справедливы равенства:

для дискретных случайных величин Р =

= ,

для непрерывных случайных величин f() = .

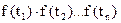Основными числовыми характеристиками n случайных величин являются математические ожидания

М() = (25)

и дисперсии

D() = = . (26)