Локальная предельная теорема Муавра-Лапласа

Пусть производится n независимых испытаний. В каждом испытании возможны два исхода: либо наступит событие A, либо 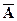. Если вероятность наступления события постоянна и равна р (0<p<1), то вероятность

= при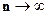

равномерно для тех m, для которых

находится в каком либо конечном интервале.

Практическое значение теоремы заключается в том, что она позволяет вычислить биноминальные вероятности Р(n,m) при большом значении n.

Теоретическое значение этой теоремы следующее: дискретное биноминальное распределение при больших значениях n можно заменить непрерывным нормальным распределением т.е. количество переходит в качество.

Пример 15. Вероятность того, что станок-автомат произведет годную деталь равна 8/9. За смену изготавливается 280 деталей. Определить вероятность того, что среди них 20 бракованных.

Решение. n=280, m=20, p=8/9, q=1/9. По формуле Бернулли эту вероятность вычислит трудно, поэтому используем локальную теорему Муавра-Лапласа:

,

где , значение - определено по таблице Приложения 1, φ(-2,11) = φ(2,11) = 0,043.