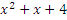Интегрирование дробно-рациональных функций

Дробно-рациональной функцией (рациональной дробью) называется отношение двух многочленов. Если степень многочлена, стоящего в числителе дроби, не меньше, чем степень многочлена в знаменателе, то в этой дроби следует выделить целую часть, т.е. представить ее в виде:

R(x) +

где R(x), P(x), Q(x) – многочлены, причем степень P(x) меньше степени Q(x). Рациональная дробь , обладающая этим свойством, называется правильной. Для интегрирования такой дроби ее необходимо разложить в сумму простейших дробей, которые легко интегрируются:

т.е. этот квадратный трехчлен не имеет действительных корней (интегрирование простейших дробей последнего типа будет показано ниже на примере). Остановимся подробнее на методике разложения правильной рациональной дроби в сумму простейших дробей. Это выполняется по следующей схеме:

1. Сначала знаменатель дроби Q(x) необходимо разложить на множители вида: x-a, (x- .

При этом часто используется теорема Виета: если квадратный трехчлен имеет корни то

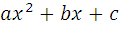= a(x- .

2. Далее следует записать разложение дроби в сумму простейших дробей, оставляя неопределенными коэффициентами А, В, С, D и т.д. При этом каждому множителю вида (x-a) соответствует дробь , множителю вида ( соответствует сумма дробей:

,

а множителю вида 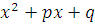, если он не имеет действительных корней (, соответствует дробь вида:

.

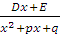3. Для определения коэффициентов A, B, C, D, E в этом разложении следует приравнять коэффициенты при одинаковых степенях x у многочлена P(x) и многочлена, который получается в числителе после приведения записанной суммы простейших дробей к общему знаменателю (метод неопределенных коэффициентов). Можно также находить эти коэффициенты путем сравнения значений указанных многочленов при конкретных значениях x (в первую очередь, при x, совпадающих с корнями знаменателя Q(x).

Вычислить интеграл:

1)

Решение. Произведем преобразования:

; , приводим к общему знаменателю.

Следовательно, , раскрываем скобки в числителе

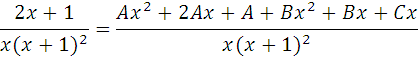
2x+1=

Приравниваем коэффициенты при x. Здесь коэффициент при в левой части равен 0, следовательно A+B=0; коэффициент при x=2, поэтому

2A+B+C=2.

Свободный член в левой части равен 1, отсюда следует, что A=1

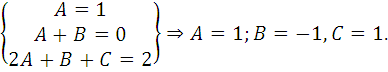
Итак,

2)

Решение:

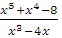Дробь является неправильной; выделим целую часть:

Решение:

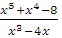Дробь является неправильной; выделим целую часть:

Таким образом, .

Прежде чем приступить к интегрированию, необходимо разложить дробь на сумму простейших дробей. В силу теоремы данная дробь может быть представлена в виде

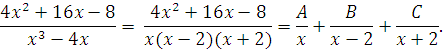
Неизвестные коэффициенты находим следующим образом

Сравнивая числители исходной дроби и дроби с неизвестными коэффициентами получаем систему трех линейных уравнений с тремя неизвестными

Итак,

.

2) ;

Решение:

Разложим дробь 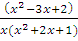на сумму простейших:

.

Неизвестные коэффициенты A,B,C находим из системы:

Итак, .

3) ;

Решение:

Дробь имеет следующее разложение на сумму простейших дробей:

.

Коэффициенты A,B,C находятся из следующей системы:

Итак,

Самостоятельно:

1) ;

2) ;

3) ;

4) ;

Ответы:

1) 2)

4)

Таким образом, .

Прежде чем приступить к интегрированию, необходимо разложить дробь на сумму простейших дробей. В силу теоремы данная дробь может быть представлена в виде

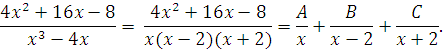
Неизвестные коэффициенты находим следующим образом

Сравнивая числители исходной дроби и дроби с неизвестными коэффициентами получаем систему трех линейных уравнений с тремя неизвестными

Итак,

.

2) ;

Решение:

Разложим дробь 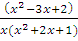на сумму простейших:

.

Неизвестные коэффициенты A,B,C находим из системы:

Итак, .

3) ;

Решение:

Дробь имеет следующее разложение на сумму простейших дробей:

.

Коэффициенты A,B,C находятся из следующей системы:

Итак,

Самостоятельно:

1) ;

2) ;

3) ;

4) ;

Ответы:

1) 2)

4)