Проектный расчет двухступенчатого соосного редуктора типа Ц2С

Редукторы Ц2С выпускаются в виде отдельного агрегата и мотор – редуктора. При этом затраты на изготовление редуктора и стоимость электродвигателя составляют свыше 80 % от всей стоимости привода, а на изготовление рамы, муфты и других деталей расходуется менее 20% средств. В этой связи повышение срока службы редуктора с обеспечением равнопрочности всех деталей является актуальной задачей.

При конструировании редуктора наилучшим образом должны быть выбраны оптимальные параметры, удовлетворяющие различным требованиям: наименьшей массе зубчатых колес и самого редуктора, стоимости, компактности, равнопрочности элементов, ограничений максимального передаточного отношения быстроходной ступени для обеспечения условии , нормальной смазки подшипников, минимальных потерь на разбрызгивание масла и т.д.

Цель работы – проведение оптимизации параметров редуктора 1Ц2С без выполнения эскизной компоновки, необходимой при обеспечении конструктивных ограничений. Это даст возможность для широкого внедрения систему автоматизированного проектирования (САПР).

В связи с появлением новых международного и российского стандартов, может быть введено отношение нагруженности и контактных напряжений ступеней. Его следует рассматривать, как отношение комплексных коэффициентов контактных напряжений ступеней, введенное профессором В.Н. Кудрявцевым при выполнении зубчатых колес из стали.

Для краткости отношения комплексных коэффициентов вводится отношение нагруженности ступеней и оно имеет вид:

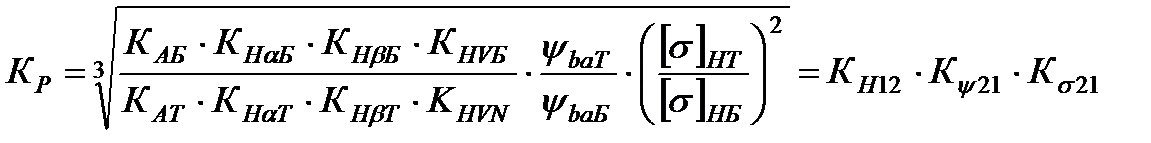(49)

где - отношение коэффициентов нагрузок быстроходной ступени к тихоходной; - отношение коэффициентов ширины относительно межцентровых расстояний тихоходной ступени к быстроходной; - отношение допускаемых напряжений тихоходной ступени к быстроходной; К _АБ = К _АТ - коэффициенты внешней динамики ступеней.

Тогда при равенстве межцентровых расстояний для двухступенчатого соосного редуктора даст следующую зависимость:

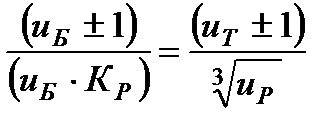(50)

Совместное решение с общеизвестным уравнением 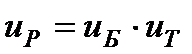даст формулу для определения передаточного числа быстроходной ступени с внешним зацеплением

; (51)

Эта формула имеет вид, как для редуктора Ц2У при К _а=1. Следовательно, между двухступенчатыми цилиндрическими редукторами по развернутой схеме и соосной с внешним зацеплением существует взаимосвязь, и можно использовать существующие теории для развернутой схемы.

Для сравнения различных теорий введем следующие относительные параметры:

Отношение передаточных чисел быстроходной ступени – u _Б к тихоходной – u _Т.

С этим параметром связана изгибная прочность зубьев колес всех ступеней. Оптимальные отношения, по исследованиям немецких ученых Г. Ниманна и В. Вольфа, находятся в пределах 1,1…1,3.

По исследованиям Дунаева П.Ф. и Леликова О.П. с отношением передаточных чисел ступеней также связана минимальная суммарная масса зубчатых колес и конструктивные ограничения.

Второй параметр - отношение диаметров колес тихоходной ступени к быстроходной, от которого зависит объем редуктора и необходимая высота погружения зубчатых колес в масляную ванну. Отношение диаметров колес через межцентровое расстояние дает уравнение:

(52)

Эта формула при К _Р = 1 дает равенство диаметров при и Таким образом, при К _Р>1 отношение диаметров будет меньше единицы.

Отношение действительной ширины контакта зубчатых колес тихоходной ступени – b _Т к быстроходной – b _Б можно получить из равенства межцентровых расстояний которое дает выражение:

(53)

Данное выражение дает возможность обеспечить контактную равнопрочность ступеней, т.е. и .

Коэффициент ширины для тихоходной ступени редукторов типа 1Ц2С рекомендуется = 0,315…0,4 при использовании улучшенных зубчатых колес, а = 0,25…0,315 из закаленных сталей.

Коэффициент ширины быстроходной ступени лучших мировых образцов редукторов типа 1Ц2С связаны следующим соотношением .

Определение передаточных чисел ступеней из условия равенства межцентровых расстоянии с использованием дает сложное уравнение со многими переменными. Графическая зависимость передаточного числа быстроходной ступени от общего передаточного числа редуктора типа Ц2С при различном значении комплексного коэффициента – приведена в учебнике по курсовому проектированию.

При = 3 передаточное число ступеней в пределах u _P = 12,5…20 равны, а при u _P = 8 передаточное число быстроходной ступени меньше тихоходного, что не соответствует реальности. При = 1 передаточное число быстроходной ступени превышает u _Б = 8 уже при u _P = 25 и выше. Следовательно, комплексный коэффициент – имеет сложную зависимость от передаточного числа редуктора.

В работах Ниберга Н.Я. приняты что является частным случаем, во – вторых, сокращение принимается с большим допущением и с учетом этих обстоятельств получена зависимость:

Для решения этого уравнения на ЭВМ предлагается определить где и

Предлагаемая зависимость требует использования ЭВМ и рекомендуемые значения С приведены в таблице. Анализ табл. 4. показывает, что отношение передаточных чисел - К _И быстроходной ступени – u _Б к тихоходной – u _Т получается постоянным, равным двум. Это дает простое решение для определения передаточных чисел ступеней и , что гораздо проще для вычисления, чем использование вышеприведенной сложной зависимости.

Формулы для определения передаточных чисел ступеней, предлагаемые Дунаевым П.Ф. и Леликовым О.П., получены из выражений и 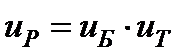. Совместное решение этих простых зависимостей дает формулу для нахождения передаточного числа быстроходной ступени

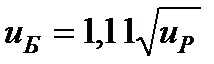(54)

Передаточное число тихоходной ступени в зависимости от общего передаточного числа редуктора - u _P имеет вид.

(55)

Приведенные формулы дают удовлетворительные практические результаты, несмотря на отсутствие глубокого теоретического обоснования.

Формула для определения передаточного числа быстроходной ступени, предлагаемая профессором Г.А. Снесаревым, имеет аналитический вывод

(56)

Как видим из данной формулы отношение нагруженности для всего диапазона передаточных чисел редуктора является постоянной величиной.

В заключении отметим, что отношения нагруженности можно получить из диаметров колес ступеней

(57)

С другой стороны для определения передаточного числа быстроходной ступени имеет выражение (51) и после подстановки в выражение (57) получим предельное значение отношения нагруженности.

(58)

Следовательно, все три составляющие отношения нагруженности зависят от общего передаточного числа редуктора.

Отношение коэффициента нагрузок К _Н12 зависит от многих факторов и из практических расчетов можно получить следующую приближенную зависимость

(59)

здесь К _АБ = К _АТ - коэффициент внешней динамики ступеней.

Следующие отношения и это инструмент для выравнивания при расчете и конструировании. Если считать оптимальным , то произведение и составляет .

Отношение допускаемых напряжений ступеней при одинаковых материалах и термообработке шестерен, а также при аналогичных условиях для колес ступеней можно получить следующее выражение:

(60)

Тогда отношение коэффициентов ширины

(61)

Результаты определения параметров редуктора типа 1Ц2С по формулам различных авторов приведены в таблице 6.

Таким образом, для определения передаточного числа быстроходной ступени на этапе проектирования предлагается выражение

(62)

Отношение коэффициентов ширины будет

(63)

Отношение диаметров колес находим по уточненной формуле

(64)

Таблица 6

u P		31,5				12,5
Параметры
По Нибергу Н.Я	С	-	-	15,8	12,9	10,7	9,0	7,61	6,37
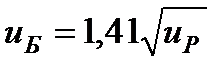
	-	-	7,1	6,3	5,6	5,0	4,5	4,0
	-	-	3,55	3,15	2,8	2,5	2,24
	-	-
	-	-	1,20	1,19	1,19	1,19	1,19	1,18
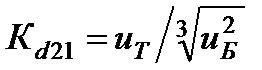
	-	-	0,98	0,96	0,94	0,90	0,85	0,8
По Дунаеву П.Ф.		7,1	6,3	5,6	5,0	4,5	4,0	3,55	3,15
	5,6	5,0	4,5	4,0	3,55	3,15	2,8	2,5
	1,23	1,23	1,23	1,23	1,23	1,23	1,23	1,23
По Снесареву Г.А..		9,4			5,8		4,2	3,5	2,9
	4,25	3,9	3,6	3,4	3,2	3,3	2,8	2,70
	2,2		1,96	1,7	1,6	1,3	1,25	1,1
	1,25	1,2	1,23	1,25	1,24	1,3	1,24	1,246
	1,12	1,11	1,1		1,14	0,81	1,2	1,22
Предлагаемая методика		7,1	6,3	5,6	5,0	4,5	4,0	3,55	3,15
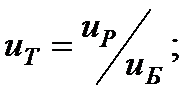
	5,6	5,0	4,5	4,0	3,55	3,15	2,8	2,5
	1,08	1,09	1,08	1,07	1,06	1,05	1,04
	0,95	0,94	0,94	0,94	0,93	0,93	0,92	0,91
	1,25	1,26	1,24	1,25	1,26	1,27	1,27	1,12