 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Редуктора передаточных чисел ступеней
|
|
Из этого выражения допускаемый момент на колесе:

где 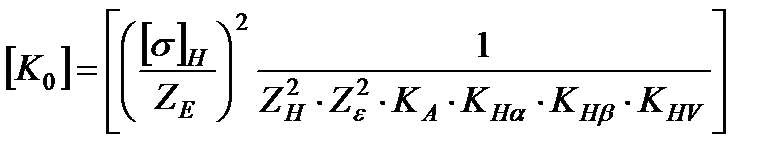 - комплексный коэффициент, учитывающий контактные напряжения, характер нагружения и механических свойств материалов зубчатой пары.
- комплексный коэффициент, учитывающий контактные напряжения, характер нагружения и механических свойств материалов зубчатой пары.
Отсюда
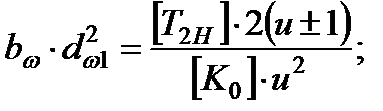 (29)
(29)
Масса зубчатой пары через объем и удельную массу –  будет
будет
 (30)
(30)
После подстановки из выражения (29)  уравнение примет вид
уравнение примет вид

или

или

где 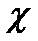 – параметр массы зубчатых колес в относительных выражениях.
– параметр массы зубчатых колес в относительных выражениях.
Для многоступенчатых передач данное выражение при умножении правой и левой части на 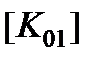 примет вид:
примет вид:

Для того чтобы найти экстремальные значения суммарной массы зубчатых передач, как функции  в которой переменные связаны между собой зависимостью
в которой переменные связаны между собой зависимостью  применен метод Лагранжа и функция ищется
применен метод Лагранжа и функция ищется 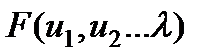 , имеющий вид
, имеющий вид

где  - неизвестный множитель.
- неизвестный множитель.
Условия экстремальных значений функций F запишется в виде

где К =1,2,3,… n.
Выражение для определения параметра суммарной массы передач упростится, если подставить значение комплексных коэффициентов для всех ступеней и считать материалы шестерен, а также всех колес одинаковыми
 (31)
(31)
здесь  - коэффициент нагрузки каждой ступени;
- коэффициент нагрузки каждой ступени;
 - допускаемый контактный предел выносливости зубчатой пары каждой ступени.
- допускаемый контактный предел выносливости зубчатой пары каждой ступени.
При  и
и  для одно-, двух- и трехступенчатых передач параметры массы зубчатых колес в относительных единицах, в зависимости от передаточного числа быстроходной ступени, приведены на рис.5, 6 и 7.
для одно-, двух- и трехступенчатых передач параметры массы зубчатых колес в относительных единицах, в зависимости от передаточного числа быстроходной ступени, приведены на рис.5, 6 и 7.
Действительно, для выражения (31) по старому стандарту ГОСТ 21354-75 отношение комплексных коэффициентов ступеней можно было принять равным единице для зубчатых передач с неограниченным сроком службы, так как правая ветвь кривой контактной усталости была горизонтальной к оси абсцисс.
Однако в новом стандарте ГОСТ 21354-87 кривой усталости по контактной прочности для левой ветви имеет показатель 6, а для правой – 20. Составляющие коэффициента нагрузки имеют большие значения и приближены к международному стандарту ISO 6336. Тогда отношение комплексных коэффициентов  будет меньше единицы, так как
будет меньше единицы, так как  и
и  . В этой связи установление отношения комплексных коэффициентов с использованием стандарта ISO 6336 ждет своего исследователя.
. В этой связи установление отношения комплексных коэффициентов с использованием стандарта ISO 6336 ждет своего исследователя.
В заключении укажем, что на основании исследования В.Н.Кудрявцева установлено, что одноступенчатый редуктор с передаточным числом u = 10 имеет массу по сравнение с двухступенчатым на 84% больше, а двухступенчатый редуктор при общем передаточном числе 63 имеет массу на 34% больше, чем трехступенчатый.
Таким образом, уменьшение и ограничение передаточных чисел быстроходной ступени и увеличение числа ступеней передач позволяет не только уменьшить массу, а также обеспечить конструктивные требования.
Формулу, предложенную проф. Г.А. Снесаревым для определения передаточных отношений двухступенчатых редукторов типа Ц2У, можно получить и другим путем - из условия обеспечения нормальной смазки зубчатых колес, а также уменьшения потерь на разбрызгивание масел (т.е. барботажные потери). Для этого достаточно принять отношение диаметров колес тихоходной ступени к быстроходной равным 1,33  . Тогда, дополнительно используя общеизвестную зависимость
. Тогда, дополнительно используя общеизвестную зависимость  , получим:
, получим:

Рис.5. Зависимость от для одноступенчатой цилиндрической передачи

Рис.6. Зависимость от и для двухступенчатой цилиндрической передачи
при  и
и 

Рис.7. Зависимость от и для трехступенчатой цилиндрической передачи
при 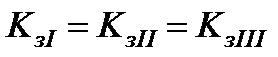 и
и 
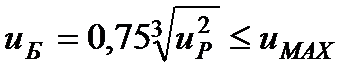 (32)
(32)
 (33)
(33)
Данные этих параметров, в зависимости от передаточного числа редуктора, занесены в таблицу 3.
Теоретические основы формул (32) и (33) по Г.А.Снесареву не приводятся, так как не соответствуют стандартам ГОСТ 21354-87 и ISO 6336. Как было указано, является частным случаем РТМ 24.090-76 ВНИИПТМаш для грузоподъемных машин, работающих в повторно – кратковременном режиме.
Исследованием редукторов типа Ц2У занимались Дунаев П.Ф. и Леликов О.П. Они минимизировали не только площадь основания корпуса – А, массы зубчатых колес – М К, длину редуктора – L и объем редуктора – V в зависимости от отношения передаточных чисел редуктора (uБ/uТ) и установили влияние его на такие конструктивные ограничения, как диаметр быстроходного вала под шестерней – d f1, расстояние между наружными кольцами подшипников быстроходной ступени -  и тихоходной -
и тихоходной -  и зазор между колесом быстроходной ступени и валом колеса тихоходной ступени -
и зазор между колесом быстроходной ступени и валом колеса тихоходной ступени -  . Для исследования был взят редуктор Т 2 = 420 Нм, u ред = 20,
. Для исследования был взят редуктор Т 2 = 420 Нм, u ред = 20,  Н/мм2.
Н/мм2.
Необходимо подчеркнуть, что такими допускаемыми напряжениями обладают зубчатая пара средней твердости, т.е. шестерни подвергнутые к закалке ТВЧ и улучшенные колеса из стали 40Х. При этом считают, что обеспечивает вышеуказанные требования отношение быстроходной ступени к тихоходной  Тогда с использованием общеизвестной зависимости
Тогда с использованием общеизвестной зависимости 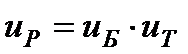 нетрудно получить формулу для определения передаточных чисел в следующем виде:
нетрудно получить формулу для определения передаточных чисел в следующем виде:
 (34)
(34)
 (35)
(35)
Зависимости межосевого расстояния -  , суммарной массы зубчатых колес – М СК, массы редуктора – М Р, диаметра впадин шестерни быстроходной ступени – d f (штрихпунктирная линия), разницы диаметров колес тихоходной ступени по сравнению с быстроходной
, суммарной массы зубчатых колес – М СК, массы редуктора – М Р, диаметра впадин шестерни быстроходной ступени – d f (штрихпунктирная линия), разницы диаметров колес тихоходной ступени по сравнению с быстроходной 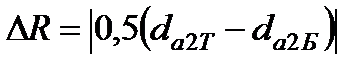 от отношении передаточного числа быстроходной ступени к тихоходной – К И приведены на рис.8.8. Здесь для сравнения взяты три группы термообработки:
от отношении передаточного числа быстроходной ступени к тихоходной – К И приведены на рис.8.8. Здесь для сравнения взяты три группы термообработки:
I - группа- термообработка зубчатых колес - улучшение.
II - группа-термообработка, закалка ТВЧ шестерни, улучшение колеса.
III - группа - термообработка, цементация шестерни, закалка ТВЧ колес.
Для сравнения и последующего приведения к новым стандартам составим сводную таблицу 4.
Таблица 4
| Методика | Параметры | u p | |||||||
| 31,5 | 12,5 | ||||||||
| По Нибергу Н.Я. | 
| 11,696 | 9,97 | 8,55 | 7,37 | 6,35 | 5,38 | ||

| 3,42 | 3,16 | 2,9 | 2,7 | 2,5 | 2,3 | |||

| 3,42 | 3,16 | 2,9 | 2,7 | 2,5 | 2,3 | |||
| 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | |||

| |||||||||
| По Вольфу В. | Из графика при
 с обеспечением
с обеспечением 
| u Б | 6,6 | 6,3 | 5,15 | 4,25 | 3,84 | 3,25 | |
| u T | 5,0 | 4,85 | 4,7 | 4,15 | 3,86 | ||||

| 1,1 | 1,09 | 1,06 | 0,90 | 0,88 | 0,84 | 0,5 | ||

| 1,77 | 1,78 | 1,69 | 1,70 | 1,63 | 1,61 | 1,66 | ||
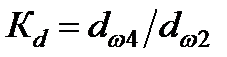
| 1,75 | 1,80 | 1,67 | 1,74 | 1,66 | 1,67 | |||
| По Ниманну Г. | Из графика при 
| uT | 7,1 | 6,3 | 5,6 | 3,55 | 2,5 | ||
| uБ | 5,6 | 4,46 | 3,52 | 3,2 | |||||
| 1,26 | 1,26 | 1,25 | 1,25 | 0,78 | |||||

| 1,7 | 1,64 | 1,59 | 1,54 | 1,6 | 1,5 | 1,2 | ||

| 1,64 | 1,58 | 1,54 | 1,48 | 1,6 | 1,53 | 1,6 | ||
| По Ниманну Г. | Из графика для практики рис.4 | uT | 7,1 | 6,5 | 5,6 | 5,15 | 3,2 | ||
| uБ | 4,4 | 3,8 | 3,3 | 2,25 | 2,43 | 2,5 | |||

| 1,6 | 1,6 | 1,7 | 1,8 | 1,96 | 2,1 | 1,28 | ||

| 1,57 | 1,49 | 1,43 | 1,36 | 1,30 | 1,25 | 1,33 | ||

| 1,47 | 1,39 | 1,3 | 1,22 | 1,24 | 1,06 | 1,25 | ||
| По Кудряв-цеву В.Н. | Из графика рис.6 | uБ | 8,5 | 7,5 | 6,25 | 5,26 | 4,5 | 3,9 | 2,75 |
| uT | 4,7 | 4,2 | 4,0 | 3,8 | 3,5 | 3,2 | 2,9 | ||
| Ки | 1,81 | 1,78 | 1,56 | 1,38 | 1,29 | 1,22 | 0,95 | ||
| Ка | 1,49 | 1,45 | 1,47 | 1,49 | 1,47 | 1,45 | 1,43 | ||
| Кd | 1,37 | 1,33 | 1,37 | 1,40 | 1,40 | 1,39 | 1,45 | ||
| По Снесареву Г.А. | 8,77 | 7,48 | 6,4 | 5,5 | 4,8 | 4,0 | |||

| 4,56 | 4,2 | 3,9 | 3,6 | 3,3 | 3,1 | 2,7 | ||

| 1,92 | 1,77 | 1,64 | 1,52 | 1,42 | 1,3 | 1,13 | ||

| 1,46 | 1,45 | 1,44 | 1,43 | 1,42 | 1,42 | 1,37 | ||
| 1,33 | 1,33 | 1,33 | 1,33 | 1,33 | 1,33 | 1,33 | |||
| По Дунаеву П.Ф. | 
| 7,18 | 6,4 | 5,7 | 5,1 | 4,5 | 4,0 | 3,2 | |

| 5,57 | 4,9 | 4,4 | 3,9 | 3,5 | 3,1 | 2,5 | ||

| 1,30 | 1,30 | 1,30 | 1,30 | 1,30 | 1,30 | 1,30 | ||

| 1,70 | 1,60 | 1,50 | 1,49 | 1,39 | 1,34 | 1,24 | ||

| 1,64 | 1,56 | 1,50 | 1,45 | 1,39 | 1,34 | 1,24 | ||
| Для всех по формуле (8.44) | Ниберг Н.Я. | 11,6 | 8,6 | 7,4 | 6,4 | 5,4 | |||
| Вольф В. | 6,6 | 6,3 | 5,2 | 4,2 | 3,8 | 3,2 | |||
| Ниманн Г. | 7,1 | 6,3 | 5,6 | 5,0 | 4,0 | 3,5 | 2,5 | ||
| Кудрявцев В.Н. | 8,5 | 7,5 | 6,2 | 5,2 | 4,5 | 3,9 | 2,7 | ||
| Снесарев Г.А. | 8,8 | 7,6 | 6,4 | 5,5 | 4,8 | 4,1 | 3,0 | ||
| Дунаев П.Ф. | 7,2 | 6,4 | 5,7 | 5,1 | 4,5 | 4,0 | 3,2 |
Безусловно, обеспечение равнопрочности зубчатых передач, подшипников качения, жесткости валов и общей надежности всей системы - задача очень сложная, при этом необходимо выдержать такие условия, как  ,
,  ,
, 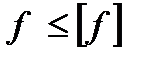 ,
,  ,
, 
Если учесть, что на 1 млн. изделий допустимы 6 отказов за планируемый срок службы, то понятны актуальность и важность любого исследования направленного на повышение надежности и вероятности безотказной работы.
Для анализа теоретических и практических данных двухступенчатых передач введем ряд безразмерных параметров, как отношение передаточных чисел – К и быстроходной ступени – u Б к тихоходной – u Т:
 (36)
(36)
Отношение межцентровых расстояний – К а тихоходной ступени -  к быстроходной -
к быстроходной -  при К Р = 1 будет
при К Р = 1 будет
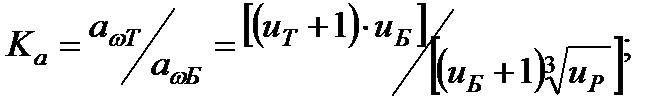 (37)
(37)
Отношение диаметров колес – К d тихоходной ступени – d KT к быстроходной – d КБ, которое при К Р = 1 определяется по выражению
 (38)
(38)
Значения новых параметров для сопоставления занесены в таблицу 3.

Рис.8. Зависимости  ,
,  ,
,  ,
,  ,
,  от
от 
Как видим, по теории Ниберга Н.Я., из условия компактности редуктора (минимального объема) не обеспечиваются такие конструктивные требования, как жесткость быстроходного вала (d f1 ³ 1,25 d) и зазор между колесом быстроходной ступени и выходным валом - 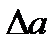 (
( > 30 мм). Поэтому им был установлен предел применимости для редукторов Ц2У, Ц2 с передаточным числом от 8 до 20.
> 30 мм). Поэтому им был установлен предел применимости для редукторов Ц2У, Ц2 с передаточным числом от 8 до 20.
Немецкий исследователь профессор Вольф В. определил из условия изгибной равнопрочности минимальное суммарное межцентровое расстояние, что важно для стальных твердых зубчатых передач. Из этой теории вытекает параметр К и, который должен иметь предел 0,84…1,1, при К а = 1,6…1,8 и К d = 1,25…1,6. Необходимо отметить, что редукторы 1Ц2у имеют К а = 1,25…1,6 и по контактной прочности К и больше указанных пределов до 1,8.
Определением минимального суммарного межцентрового расстояния из условия изгибной прочности занимался профессор Ниманн Г. По его данным К и = 1…1,25, К а = 1,5…1,7, К d = 1,48…1,64. Однако учитывая, что при расчете на контактную прочность зубчатых передач модуль принимается конструктивно и изгибные напряжения получаются намного меньше допускаемого, поэтому для практики нетрудно получить по формулам (8.36; 8.37; 8.38) К а = 1,25…1,6, К d = 1,06…1,45 для u Р = 8…40, при этом К и = 2,1…1,6, намного больше К и = 1,25 (рис. 8.4).
Определением минимальной суммарной массы зубчатых колес из условия контактной прочности, как было указано раньше, с использованием старого стандарта ГОСТ 21354-75, занимался профессор Кудрявцев В.Н. При этом К и = 1,22…1,8, К а и К d почти постоянные величины)  и
и  .
.
Таким образом, величина зазора между колесом быстроходной ступени и выходным валом – 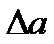 зависит не только от К и, но и от К а.
зависит не только от К и, но и от К а.
Как было указано, исследованием редукторов типа 1Ц2У и 2Ц2 (обозначение рекомендуемое Снесаревым Г.А.) занимался профессор Снесарев Г.А. При этом для определения передаточных чисел ступеней выдвинуты два условия К d = 1,33 для ограниченного срока службы и К d = 1,11 для не ограниченного срока службы, поэтому из условия контактной равнопрочности ступеней при и К рн = 1 для первого случая формулы имеют вид:  и
и  , а для второго случая
, а для второго случая  и
и  . Данные для первого случая сведены в таблицу 8.3, при этом К а = 1,37…1,46, К d = 1,33, К и = 1,13…1,92 для u Р = 8…40. Как видим, по теории Кудрявцева В.Н. и Снесарева Г.А. ограничение К и = 1, 3 Дунаева П.Ф. и Леликова О.П. не выдерживается, следовательно, параметрическая оптимизация многоступенчатых редукторов очень сложна и зависит при прочих равных условиях от величины крутящего момента.
. Данные для первого случая сведены в таблицу 8.3, при этом К а = 1,37…1,46, К d = 1,33, К и = 1,13…1,92 для u Р = 8…40. Как видим, по теории Кудрявцева В.Н. и Снесарева Г.А. ограничение К и = 1, 3 Дунаева П.Ф. и Леликова О.П. не выдерживается, следовательно, параметрическая оптимизация многоступенчатых редукторов очень сложна и зависит при прочих равных условиях от величины крутящего момента.
В исследованиях Дунаева П.Ф. и Леликова О.П. для определения передаточных чисел ступеней редукторов типа Ц2У и Ц2 по развернутой схеме были получены К и = 1,3 для частного случая при u Р = 20 для обеспечения минимальной суммарной массы зубчатых колес и конструктивных ограничений.
Действительно, по теории Кудрявцева В.Н. при К и = 1,38 и u Р = 20 обеспечивается минимальная масса зубчатых колес. Однако с изменением передаточного числа редуктора для u Р = 8…40, отношение передаточных чисел ступеней изменяется от 1,22 до 1,81, что вытекает из графика Ниманна Г. при обеспечении изгибной прочности зубьев ступеней.
В новом учебнике по конструированию узлов и деталей К и = 1,3 рекомендуется для обеспечения разницы радиусов колес ступеней –  >30 мм, где указывается, что это необходимо для уменьшения потерь на разбрызгивание масла.
>30 мм, где указывается, что это необходимо для уменьшения потерь на разбрызгивание масла.
В заключении отметим, что профессор Ниманн Г., понимая сложность рассматриваемой проблемы для определения передаточных чисел ступеней редукторов типа Ц2У и Ц3У, предложил графическую зависимость (рис.4).
Как известно, межосевое расстояние, определенное из контактной прочности, намного больше, чем по изгибным напряжениям зубчатой передачи, поэтому Ниманн Г. установил верхнюю и нижнюю границу передаточного числа быстроходной ступени для редукторов Ц2У, где пунктирная линия для твердых зубчатых передач, которая параллельна штрихпунктирной линии, полученной из теории по изгибной прочности. Для зубчатых передач мягкой твердости передаточное число быстроходной ступени больше и к теоретическому положению имеет некоторый наклон. Графическая зависимость приводится также в учебнике профессора Иванова М.Н. по деталям машин.
Следует подчеркнуть, что вышеизложенная параметрическая оптимизация проведена на основе старого стандарта, где правая ветвь кривой выносливости Вёлера параллельна оси абсцисс.
На основе нового стандарта ГОСТ 21354-87, для теоретического положения Ниберга Н.Я. можно получить следующие формулы:
Передаточное число быстроходной ступени
 ; (39)
; (39)
Передаточное число тихоходной ступени
 ; (40)
; (40)
Отношение передаточных чисел ступеней
 ; (41)
; (41)
Отношение межцентровых расстояний
 ; (42)
; (42)
Отношение диаметров колес
 ; (43)
; (43)
Как видно, по приведенным формулам (39 – 43) определить параметры проектируемого редуктора невозможно, так как неизвестен коэффициент нагруженности редуктора (и желаемой долговечности) – К Р. С другой стороны задача может быть решена методом последовательных приближений (итераций).
На основе анализа существующих конструкций редукторов 1Ц2У, можно обнаружить следующее: во – первых, с крутящим моментом на выходе до 10 тысяч Нм редукторы имеют передаточное число до 41, а при крутящем моменте свыше 10 тысяч Нм общее передаточное число доходит до 50. Следовательно, конструктивные ограничения косвенно зависят также от величины крутящего момента. Таким образом, применение врезной вал – шестерни для быстроходной ступени возможно при значительном крутящем моменте.
Произведение коэффициента нагруженности редуктора – К РН на отношение межцентровых расстоянии приближенно составляет  тогда передаточное отношение быстроходной ступени будет
тогда передаточное отношение быстроходной ступени будет
 (44)
(44)
Для определения передаточного числа тихоходной ступени и отношения передаточных чисел редуктора можно использовать общеизвестную зависимость  и
и 
Отношение межцентровых расстояний определяется по формуле (42), а диаметров колес – по формуле (43).
Как было указано раньше коэффициент нагруженности редуктора по изгибной прочности

Учитывая данное обстоятельство Ниманном получено  тогда передаточное число быстроходной ступени будет
тогда передаточное число быстроходной ступени будет
 (45)
(45)
Передаточное число тихоходной ступени будет
 (46)
(46)
Отношение межосевых расстояний:
 (47)
(47)
Отношение диаметров колес
 (48)
(48)
Отношение передаточных чисел ступеней

Для сравнения различных методик расчета на основе нового стандарта составили новую таблицу 5.
По новому стандарту ГОСТ 21354-87 и ISO 6336 коэффициент нагруженности редуктора по контактной прочности – К рН изменяется от 1,2 до 1,3 при u P = 8…48, а коэффициент нагруженности редуктора по изгибной прочности K pF = 0,98…0,96.
Дата публикования: 2014-10-19; Прочитано: 1415 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
