Проектный расчет параметров цилиндрических двухступенчатых редукторов типа Ц2У, Ц2 общего назначения

Теоретические основы проектного расчета по определению передаточного отношения каждой ступени многоступенчатых цилиндрических передач по развернутой схеме из условий равнопрочности и компактности известны с 60-х годов.

Равенство диаметров колес ступеней редукторов типа Ц2У при обеспечении компактности даст следующее уравнение:

(11)

здесь - коэффициент загруженности редуктора по контактному напряжению.

Совместное решение (11) и общеизвестной зависимости общего передаточного числа редуктора - u _p:

; (12)

при К _р=1 даст следующее решение:

Передаточное число быстроходной ступени

(13)

Передаточное число тихоходной ступени

(14)

Действительно, согласно старому стандарту ГОСТ 21354-75 при неограниченном сроке службы редуктора, коэффициенты долговечности зубчатых колес были равны единице, так как правая ветвь кривой выносливости Велера была параллельна к оси абсцисс. Значение коэффициентов нагрузки - К _н были меньше, чем по стандарту ISO 6336. При равенстве коэффициентов ширины колес _, коэффициент нагруженности редуктора по контактному напряжению был близок к единице.

Необходимо отметить, что при и 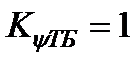рассуждение о равенстве коэффициентов отношения ширины колеса к диаметру шестерни не имеет места.

Как указывает В. Вольф, одна из задач, возникающих при конструировании многоступенчатых редукторов, заключается в выборе такого распределения передаточных чисел между ступенями, которое обусловило бы минимальные размеры редуктора. Существенным показателем, определяющим габариты редуктора с цилиндрическими колесами, является сумма межосевых расстояний между валами.

Межцентровое расстояние для одноступенчатого редуктора определяется из выражения

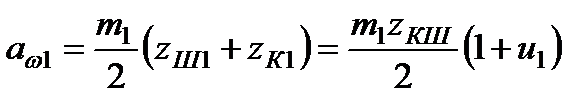
Сумма межосевых расстояний для многоступенчатой передачи

(15)

В предположении, что число зубьев шестерен в каждой ступени одинаково, то есть принимая, что Z_ш1= Z_ш2= Z_ш3= Z_ш4, выражение (15) примет вид

(16)

Модули зубьев могут быть определены из условия изгибной прочности:

(17)

где Т _ШF - расчетный крутящий момент на шестерне в Нмм;

- коэффициент нагрузки при расчете на изгибную выносливость;

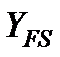- коэффициент формы зуба;

диаметр начальной окружности шестерни в мм;

ширина зубчатого колеса, выраженная через число модулей.

Из уравнения (17) модуль передачи будет

(18)

Соотношение модулей двух последовательных ступеней при Z _ш1= Z _ш2 и (рис. 1)

(19)

здесь - отношение коэффициентов нагрузки при изгибе зубьев тихоходной ступени к быстроходной;

- отношение допускаемого напряжения шестерни быстроходной ступени к тихоходной.

Следует отметить, что и , так как и правая ветвь кривой усталости имеет некоторый наклон, поэтому произведение этих величин меньше единицы, но извлечение из него кубического корня дает величину близкую к единице.

Подставляя выражение (19) в уравнение (16) получают величину суммарного межцентрового расстояния

(20)

Как известно, общее передаточное число механизма будет

; (21)

Для того, чтобы найти экстремальные значения суммарного межцентрового расстояния, как функции от передаточного числа ступеней (а_wc=f (u₁; u₂, u₃,... u_к), в которой переменные u₁, u₂, u₃... u_к связаны между собой зависимостью применим метод Лагранжа. Функция ищется в виде уравнения:

(22)

где - неизвестный множитель.

Условия экстремальных значений функции F имеют вид:

(23)

где К= 1,2… n

Решение для двухступенчатого редуктора дает следующую зависимость между передаточными отношениями при

(24)

Совместное решение с уравнением дает выражение

(25)

Решение данного уравнения на ЭВМ представлено на рис. 2 в виде графика.

Выражение (20) может иметь другой вид

(20,а)

Зависимость суммарного межцентрового расстояния в относительных единицах для двухступенчатого редуктора типа Ц2У от передаточного числа быстроходной ступени показана на рис. 3. График при передаточных числах редуктора от 8 до 40 имеет ярко выраженный минимум. Зависимость передаточного числа тихоходной ступени от общего передаточного отношения редуктора показана на рис. 2.

С точки зрения минимума суммарного межцентрового расстояния представляет интерес определение границы целесообразного перехода с одноступенчатого редуктора на двухступенчатый, с двух- на трехступенчатый и т.д.

Для одноступенчатого редуктора межцентровое расстояние составляет

(26)

для двухступенчатого

(27)

Приравнивание дает условие, определяющее границу перехода в виде:

(28)

Это уравнение, с учетом выражения (25), дает предельное отношение u =8,64 для одноступенчатого редуктора из условия изгибной прочности зубьев, выше которого целесообразен переход на двухступенчатый редуктор, независимо от числа зубьев шестерни.

Аналогично установлены границы перехода с двух на трехступенчатую схему, начиная с u =41,1 а при u =160 на четырехступенчатую схему.

Исследованием многоступенчатых редукторов по развернутой схеме занимался также профессор Ниманн Г.. Из условий изгибной прочности и минимального суммарного межцентрового расстояния для двух- и трехступенчатых редукторов передаточное число быстроходной ступени, а для трехступенчатой схемы также передаточное число промежуточной ступени показаны штрихпунктирной линией на графике рис.4. Ранее рекомендованные области по проектированию многоступенчатых передач для практики заштрихованы, и как видим, имеют завышенные значения передаточных чисел ступеней.

Следует отметить, что для трехступенчатых передач при общем передаточном числе до 100 передаточное число быстроходной ступени меньше промежуточной.

Согласно ГОСТ 21354-87, контактная выносливость зубчатых передач определяется по формуле:

Рис. 1 Рис.2

Рис.3

Рис. 4. Зависимость от общего передаточного числа