Ысқаша мазмұны. 1.Бірінші ретті дербес туындылы дифференциал теңдеудің жалпы түрі былай жазылады:

1. Бірінші ретті дербес туындылы дифференциал теңдеудің жалпы түрі былай жазылады:

(1)

Мұндағы 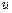- белгісіз функция, - тәуелсіз айнымалылар. - кейбір облысында екі рет үздіксіз дифференциалданатын функция болсын.

Анықтама. Кейбір облысында анықталған үздіксіз дифференциалданатын функциясы (1) теңдеудің шешімі деп аталады, егер ол төмендегідей шарттарды қанағаттандырса:

1)

2)

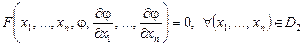
Бұл функциясы - кеңістігінде кейбір

бетті анықтайды. Осы бетті берілген теңдеудің интегралдық беті деп атайды.

Бірінші ретті дербес туындылы теңдеулерді интегралдау әдетте жәй дифференциал теңдеулер жүйесін интегралдауға келтіріледі. Сондықтан, мұндай теңдеулер жәй дифференциал теңдеулер бағдарламасына енгізілген.

Біз бұл жерде бірінші ретті дербес туындылы теңдеулердің тек

екі сызықты түрін ғана қарастырамыз.

2. Алдымен, біртекті сызықты теңдеуді қарастырайық:

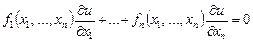(2)

Мұндағы, - функциялары кейбір 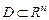облысында үздіксіз

дифференциалданатын және бәрі бірдей нөлге айналмайтын

функциялар деп есептелінеді. Бұл (2) теңдеуге төмендегідей жәй дифференциал теңдеулердің симметриялық түрі сәйкес қойылады.

(3)

Осы жүйені (2) теңдеудің сипаттаушы жүйесі деп атайды. Оның интегралдық қисықтары (2) теңдеудің сипаттауыштары (характеристикалары) деп аталады. Бұл жүйенің барлық уақытта шешімдері бар және ол жалғыз. Сондықтан, 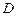облысының әрбір нүктесі арқылы тек бір ғана сипаттауыш өтеді және олардыңғ тәуелсіздерінің саны - ге тең, себебі, ол - ретті қалыпты жүйеге эквивалент.

Теорема-1. 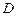облысында анықталған үздіксіз дифференциалданатын функциясы (2) теңдеудің шешімі болуы үшін оның (3) жүйенің интегралы болуы қажетті және жеткілікті.

Дәлелдеуі. 1) қажеттілігі. Айталық, функциясы (2) теңдеудің шешімі болсын:

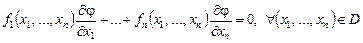(4)

Бұл функцияның толық дифференциалы былай жазылады:

(5)

Осындағы әрбір -дің орнына оған пропорционал функциясын қойсақ, төмендегідей қатынас аламыз:

(6)

Мұндағы, - пропорция коэффициенті. Алдыңғы (4) тепе-теңдікті ескерсек, квадрат жақшаның ішіндегі өрнек нөлге тепе-тең болады, яғни

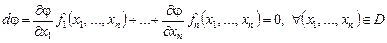(7)

Ал бұл тепе-теңдік функциясының (3) жүйенің интегралы болатынын білдіреді.

2) жеткіліктілігі. Айталық, функциясы (3) жүйенің интегралы болсын:

(8)

Соңғы тепе-теңдік функциясының (2) теңдеудің шешімі екенін көрсетеді.

Теорема-2. Берілген (2) теңдеудің жалпы шешімі

(9)

түрінде анықталады. Мұндағы, - кез келген үздіксіз дифференциалданатын функция, ал 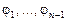- (3) жүйенің тәуелсіз интегралдары.

Дәлелдеуі. Айталық, кейбір функциясы (2) теңдеудің 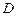облысындағы кез келген шешімі болсын. Бұл шешім 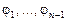функцияларымен қоса (2) теңдеуді тепе-теңдікке айналдырады:

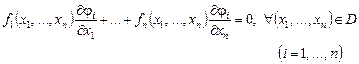(10)

Бұл біртекті сызықты жүйенің нөлдік емес

шешімі бар. Сондықтан, бұл жүйенің анықтауышы нөлге тең. Ол функцияларының якобианына тең.

(11)

Соңғы қатынас функцияларының өзара тәуелділігін көрсетеді. Олардың алдыңғы 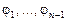функциялары өзара тәуелсіз функциялар еді. Сондықтан тәуелділікті соңғы функциясы беріп тұр:

(12)

Мұндағы, - кез келген шешім боғандықтан, (12) қатынас жалпы шешімді береді.

3. Біртексіз сызықты теңдеуді қарастырайық:

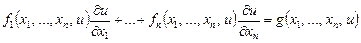(13)

Мұндағы, - функциялары кейбір облысында үздіксіз дифференциалданатын және бәрі бірдей нөлге тең емес деп есептелінеді:

Бұл теңдеуді біртекті сызықты түрге келтіру арқылы интегралдайды. Ол үшін шешімді айқындалмаған функция түрінде іздейді:

(14)

Мұндағы, - функциясын облысында үздіксіз дифференциалданатын және деп аламыз. Осы қатынасты кез келген бойынша дифференциалдайық:

Осыдан

(15)

(15) өрнекті (13) теңдеуге қойып, оны бөлшегіне көбейтсек,

(16)

теңдеуін аламыз. Бұл бойынша біртекті сызықты теңдеу. Сондықтан, алдыңғы пунктте көрсетілген тәсілді қолданамыз. Бұл теңдеудің сәйкес сипаттаушы жүйесі

(17)

түрінде жазылады. Бұл жүйенің өзара тәуелсіз интегралдары - ге тең:

Бұл жағдайда (13) теңдеудің жалпы шешімі

(18)

түрінде жазылады. Шешімді анықталмаған түрде іздеп отырғанымызды ескерсек,

(19)

қатынасын аламыз. Осындағ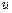ы -ды арқылы өрнектеуге мүмкін болса, ол функция (13) теңдеудің шешімі болады.

Бұл жерде арнайы шешімдер де болуы мүмкін. Ондай шешімдер сол уақытта пайда болады, егер (14) тепе-теңдік тек болғанда ғана орындалса.

4. Біртекті және біртексіз сызықты теңдеулер үшін Коши есебі былай қойылады:

теңдеудің шешімдерінің ішінен оның бір аргументі тұрақталған жағдайда белгілі бір - өлшемді бетке айналатын дербес шешімді анықтау керек, яғни шешімінің болғанда белгілі функциясына тең болатын шешімді табу керек. Мұны қысқаша

(20)

түрінде жазады.

Мысалы, екі өлшемді дербес туындылы

теңдеуі үшін Коши есебі былай қойылады:

шешімінің болғанда шартын қанағаттандыратын шешімді іздеу. Ол барлық интегралдық беттердің ішінен қисығы арқылы өтетін бетті табу болып есептелінеді.

Жалпы жағдайда Коши есебінің шешімін табу қиындық тудырмайды.