Біртексіз сызықты жүйелер

3.1. Біртексіз сызықты теңдеулер жүйесін қарастырайық:

(1)

Айталық, кейбір функциясы (1) жүйенің дербес шешімі болсын. Осы жүйеге

(2)

түрінде алмастыру жасайық. Екі жағынан да туынды алып, сол жүйенің өзін пайдалансақ, төмендегідей теңдік аламыз:

Ал бұдан шығатыны

(3)

Бұл біртекті сызықты жүйе. Осы жүйенің жалпы шешімін тауып, оны (2) қатынастағы 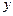-тің орнына қойсақ, (1) жүйенің жалпы шешімін табамыз.

Қорытындылап айтсақ, біртексіз жүйенің жалпы шешімі осы жүйенің дербес шешімі мен оның сәйкес біртектісінің жалпы шешімінің қосындысына тең.

Ал біртекті (3) жүйенің жалпы шешімі

(4)

түрінде жазылатыны белгілі. Мұндағы, - (3) жүйенің фундаменталь матрицасы, 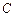- бір бағаналы матрица. Сондықтан, (1) жүйенің жалпы шешімі

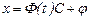(5)

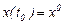түрінде жазылады. Бұл шешімнің жалпы шешім болатынын көрсету үшін одан кез келген Коши есебінің шешімін алуға болатынын дәлелдесек, жеткілікті. Ол үшін болғанда болатын шартты қанағаттандыратын векторды табу мүмкіншілігін қарастырайық:

(6)

Теңдіктегі 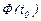фундаменталь матрица болғандықтан, 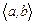аралығындағы кез келген нүктеде оның анықтауышы нөлге тең емес, яғни оның кері матрицасы бар. Сондықтан,

(7)

Осы векторды (5) қатынасқа қойып, керекті шешімді аламыз:

немесе

(8)

Мұндағы, 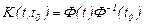- Коши функциясы.

3.2. Біртексіз сызықты жүйенің жалпы шешімін табу үшін әдетте, тұрақтыларды вариациялау әдісі қолданылады. Мұны Лагранж әдісі деп те атайды. Ол үшін біртекті жүйенің жалпы шешіміндегі тұрақты 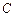векторын - ға байланысты функция деп, біртексіз жүйенің шешімін

(9)

түрінде іздейміз. Екі жағынан туынды алып, берілген (1) жүйені пайдаланып, мынандай теңдеу аламыз:

Ал

(10)

тепе-теңдігін ескерсек, онда

Осыдан

(11)

Бұл теңдеудің шешімі интегралдау арқылы былай жазылады:

(12)

мұндағы, - тұрақты вектор. Табылған - ның мәнін (9) – қатынасқа қойып, біртексіз (1) жүйенің жалпы шешімін табамыз:

(13)

Бұл жалпы шешімдегі тұрақты - векторын анықтау үшін формулада деп алсақ, онда . Сондықтан

(14)

немесе Коши функциясын енгізсек, онда шешім мына түрде жазылады:

(15)

Бұл қатынас Коши формуласы деп аталынады. Осындағы фундаменталь матрицасы нүктесінде нормаланған болса, яғни болса, онда формула мына түрде жазылады:

Егер 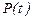матрицасы тұрақты болса, яғни - тұрақты болса және болса, онда . Бұл жағдайда жалпы шешім мына түрде жазылады:

(16)

Соңғы формулада 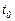- тұрақталған сан деп, ал 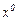- векторын кез келген тұрақты вектор деп қарастырсақ, онда (16) формула Коши түріндегі жалпы шешімді білдіреді.

3.3. Тұрақты сандарды вариациялаудың екінші түрін келтірейік.

Біртексіз жүйенің жалпы және дербес шешімін іздегенде векторын координаттары бойынша іздеген қолайлы. Олардың туындылары сызықты алгебралық жүйенің шешімдері ретінде анықталады.

Айталық, 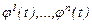вектор - функциялары (3) жүйенің фундаменталь шешімдер жүйесі болсын. Онда осы жүйенің жалпы шешімі

түрінде жазылады. Мұндағы, - еркін тұрақтылар.Енді (1) жүйенің жалпы шешімін табу үшін осы - лерді - ға байланысты үздіксіз дифференциалданатын белгісіз функциялар деп есептейік, яғни

(17)

Егер осы вектор-функцияны (1) жүйеге қойсақ, белгісіз және оның туындысы бойынша төмендегідей векторлық теңдеу алынады:

Осыдан, екенін ескерсек,

(18)

түріндегі векторлық теңдеу аламыз. Оны координаттары бойынша ашып жазсақ, төмендегідей скалярлық теңдеулер жүйесін аламыз:

(19)

Бұл жүйе алгебралық сызықты біртексіз жүйе. Ал оның негізгі анықтауышы Вронский анықтауышы болғандықтан, ол нөлге тең емес. Крамер ережесі бойынша барлық функциялары бір мәнді болып анықталады:

(20)

Осыдан

(21)

Бұл функцияларды (17) қатынасқа қойсақ,

(22)

түріндегі (1) жүйенің жалпы шешімін аламыз. Мұндағы, бірінші қосынды біртекті (3) жүйенің жалпы шешімін береді де, екінші қосынды (1) жүйенің дербес шешімін береді. Сонымен, бастапқы тұжырымға қайта келдік: біртексіз сызықты жүйенің жалпы шешімі сәйкес біртекті жүйенің жалпы шешімі мен біртексіз жүйенің дербес шешімінің қосындысынан тұрады.