Сызықты жүйенің орнықтылығы

4.1. теңдеуден тұратын тұрақты коэффициентті сызықты біртекті жүйені қарастырайық:

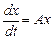(1)

Бұл жүйенің теңбе-теңдік қалпы 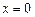нүктесінің орнықтылық, орнықсыздық шарттарын келтірейік.

Теорема-1. Егер 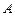матрицасының барлық меншікті сандарының нақты бөліктері теріс болса, онда (1) жүйенің теңбе-теңдік қалпы асимптотикалы орнықты, ал егер сол меншікті сандардың ең болмағанда біреуінің нақты бөлігі оң болса, онда теңбе-теңдік қалып орнықсыз.

Дәлелдеуі. Айталық, 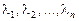- сандары 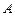матрицасының меншікті сандары болсын және 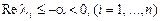. Бұл жағдайда Ляпунов функциясын құру үшін 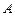матрицасын алдын ала диагоналды дерлік түрге келтіреміз. Алгебрадан белгілі, 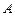матрицасы үшін кейбір 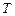матрицасын табуға болады және ол мынандай теңдікті қанағаттандырады:

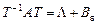
Мұнда 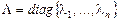, ал 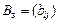- матрицасының әрбір элементі 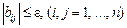шартын қанағаттандырады.

(1) жүйе үшін 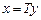алмастыруын қолдансақ,

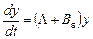(2)

жүйесіне келеміз. Осы жүйеге Ляпунов функциясын төмендегідей түрде алайық:

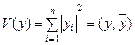(3)

Бұл функция 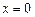нүктесінің (немесе 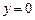нүктесінің) кез келген аймағында анықталған оң таңбалы. Енді оның туындысын есептейік:

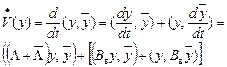
Осындағы бірінші қосындыны бағаласақ,

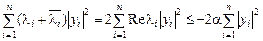
теңсіздігін аламыз. Екінші қосындыны бағалайық:

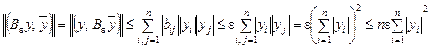Осыдан

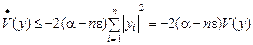(4)

Соңғы қатынастағы 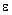санын 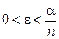теңсіздігі орындалатындай етіп алсақ, онда 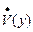функциясының анықталған теріс таңбалы болатынын көреміз. Сондықтан, Ляпуновтың екінші теоремасы бойынша теңбе-теңдік қалып асимптотикалы орнықты.

Теореманың екінші бөлігіне келетін болсақ, кейбір 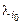меншікті санның нақты бөлігі оң болсын: 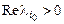. Бұл санға сәйкес шешім

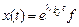(5)

түрінде жазылады. Мұндағы, 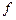- сәйкес меншікті вектор. Осыдан

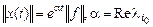(6)

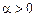болғандықтан, шексіздікке ұмтылғанда 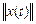нөлге ұмтылмайды, яғни теңбе-теңдік қалып орнықсыз.

Ескерту-1. Егер 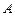матрицасының меншікті сандарының нақты бөліктері нөлге тең болып, қалғандарының нақты бөліктері теріс болса, онда теңбе-теңдік қалып орнықты да, орнықсыз да болуы мүмкін. Егер таза жорамал санға сәйкес жордан шаршысының реті бірден аспаса, онда теңбе-теңдік қалып орнықты. Кері жағдайда теңбе-теңдік қалып орнықсыз.

Мысалы, 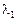меншікті саны таза жорамал сан болса, ал оған екінші ретті жордан шаршысы сәйкес келсе, онда шешім

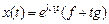(7)

түрінде жазылады. Мұндағы, 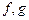- тұрақты меншікті векторлар. Осыдан

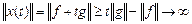егер ,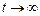

яғни теңбе-теңдік қалып орнықсыз.

Ескерту-2. Жоғарыда айтылған тұжырымдарды (1) жүйенің айқын шешімін пайдаланып дәлелдеуге де болады. Ол шешім былай жазылады:

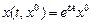(8)

Мұнда тек 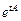матрицасының түрін анықтау керек. Жоғарғы әдістің бір артықшылығы – оны сызықты емес жүйеге де қолдануға болатындығы.

Соңғы екі тұжырымның дәлелдеулерін [4] оқу құралынан көруге болады.