Бірінші ретті сызықты теңдеулер

3.1. Белгісіз функция мен оның туындысы сызықты түрде, яғни бірінші дәрежеде байланысқан теңдеуді сызықты дифференциалдық теңдеу деп атайды. Сызықты теңдеудің келтірілген түрін қарастырайық:

(1)

Мұнда p(x), q(x) функциялары кейбір <a,b> аралығында анықталған және үздіксіз деп есептелінеді. Егер q(x)¹0 болса, онда (1) теңдеуді біртексіз сызықты теңдеу деп, ал q(x)=0 болса, онда біртекті сызықты теңдеу деп атайды:

(2)

Көбінесе (2) теңдеуді (1) теңдеудің сәйкес біртектісі деп атайды.

Біртекті (2) теңдеу айнымалылары ажыратылатын теңдеу. Екі жағын у -ке бөліп, мынандай теңдеу аламыз:

Осы қатынасты интегралдасақ:

өрнегін аламыз. Логарифмсіз жазсақ,

(3)

түріндегі (2) теңдеудің жалпы шешімін аламыз. Егер y=0 жағдайды қарастырсақ, ол осы жалпы шешімнің С=0 болғандағы мәніне сәйкес келетін шешім. Сондықтан y=0 – дербес шешім. Оны нөлдік немесе тривиaл шешім деп те атайды және ол барлық уақытта бар шешім.

Біртекті (2) теңдеудің (3) жалпы шешімін Коши түрінде жазсақ, былай жазылады:

(4)

мұнда х₀ -тұрақты сан, ал у ₀ – кез келген сан деп есептелінеді.

Біртекті теңдеу шешімдерінің екі қасиетін атап өтейік:

1⁰. Егер у ₁ және у ₂ функциялары (2) теңдеудің шешімдері болса, онда олардың қосындысы: у=у ₁+ у ₂ функциясы да сол теңдеудің шешімі болады.

2⁰. Егер у ₁ функциясы (2) теңдеудің шешімі болса, онда функциясы да (С – кез келген сан) сол теңдеудің шешімі болады.

3.2. Енді берілген біртексіз (1) теңдеуге оралатын болсақ, оның жалпы шешімін табу үшін мынандай әдістерді қолдануға болады.

1⁰. Тұрақты санды вариациялау әдісі (Лагранж әдісі).

Біртексіз (1) теңдеудің жалпы шешімін біртекті (2) теңдеудің жалпы шешімі – (3) түрде іздейміз, бірақ мұндағы С санын х -қа байланысты айнымалы функция деп есептейміз:

(5)

Осы функцияны (1) теңдеуге апарып қоялық:

.

Бұдан

теңдеуін аламыз. Енді осы теңдеуді интегралдасақ, онда

(6)

өрнегін аламыз. Мұнда С ₀ – кез келген тұрақты сан. Осы (6) өрнекті (5) қатынасқа апарып қойсақ, онда біртексіз (1) теңдеудің жалпы шешімін аламыз:

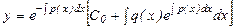(7)

Соңғы шешімді Коши түрінде жазсақ, онда мынандай өрнек аламыз:

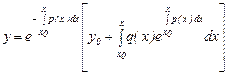(8)

мұнда х ₀-тұрақты сан, ал у₀ – кез келген сан деп есептейміз.

2⁰. Бернулли әдісі.

Біртексіз (1)теңдеудің шешімін y=u(x)v(x) түрінде іздейміз. Сонда

(9)

Мұндағы, u(x) функциясын біртекті теңдеудің шешімі түрінде алсақ, онда (9) қатынастан

теңдеуін аламыз. Осыдан интегралдау арқылы

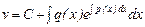(10)

болатынын көреміз. Мұнда С – тұрақты сан. Табылған және функцияларының көбейтіндісі y(x) функциясын беретін болғандықтан,

,

яғни жалпы шешім (7) түрге келеміз.

3⁰. Интегралдаушы көбейткіш әдісі (Эйлер әдісі).

Берілген біртексіз (1) теңдеудің екі жағын функциясына көбейтіп, ықшамдап жазатын болсақ, онда мынандай қатынас аламыз:

.

Осы қатынасты интегралдасақ:

,

ал бұдан

.

Тағы да жалпы шешім – (7) түрге келдік.

Жалпы, белгілі бір теңдеудің шешімін іздегенде жоғарыда келтірілген әдістердің есептеу жолын қайталамай-ақ, дайын (7) өрнекті пайдалану керек.